벡터로 이루어진 합성함수의 도함수는 어떻게 표현할 수 있는지 알아보자.
지난 시간에 벡터 X, W에 대한 합성함수 f(X, W)를 아래와 같이 정의했었다.

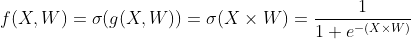
1. 도함수 ∂f/∂X , ∂f/∂W 구하기
입력 변수는 X, W 두개이므로 각각에 대한 도함수 ∂f/∂X , ∂f/∂W 를 구하면 된다.
체인룰을 이용하여 구해보자
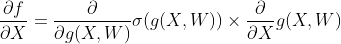

즉, ∂g/∂X , ∂g/∂W 를 구해야 한다는 것이다. (앞의 부분은 sigmoid 자체를 미분하면 되므로 쉽다)
∂g/∂X 에 대하여 각 요소를 구해보면



이렇게 표현할 수 있으므로 ∂g/∂X 를 구해보면

X에 대한 편미분이므로 W를 상수취급한다. 즉 결과는 아래와 같다.

W행렬의 전치행렬(transpose matrix)이다. 즉, W의 shape가 (a, b)였다면 W의 전치행렬은 (b, a)가 된다.
마찬가지로 ∂W를 정의하고 구해보면 ∂g/∂W는 X의 전치행렬이다.
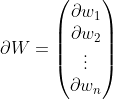
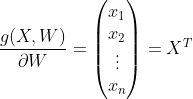
numpy의 transpose 메소드를 이용하여 전치행렬을 만들 수 있는데 parameter는 스스로 알아보자.
아래 파이썬 코드는 transpose 메소드 사용 결과이다.
import numpy as np
X = np.array([[1, 2, 3]])
W = np.array([[3],
[2],
[1]])
X = np.transpose(X, (1, 0))
W = np.transpose(W, (1, 0))
print('X transpose', X)
print('W transpose', W)
"""
실행결과
X transpose [[1]
[2]
[3]]
W transpose [[3 2 1]]
"""
도함수를 구하는 파이썬 코드이다.
def deriv(func, input, delta=0.001):
return (func(input + delta) - func(input)) / delta
def matrix_sigmoid_deriv(X, W, func_list):
f1 = func_list[0] # matmul
f2 = func_list[1] # sigmoid
F1 = f1(X, W)
#∂(f2(f1))/∂(f1)
df2f1_df1 = deriv(f2, f1(X, W))
#∂(f1)/∂X
df1_dX = np.transpose(W, (1, 0))
#∂(f1)/∂W
df1_dW = np.transpose(X, (1, 0))
#∂(f2(f1))/∂x = ∂(f2(f1))/∂(f1) X ∂(f1)/∂x
#∂(f2(f1))/∂y = ∂(f2(f1))/∂(f1) X ∂(f1)/∂y
return df2f1_df1*df1_dX, df2f1_df1*df1_dW
2. 결과 확인하기
도함수가 제대로 맞는지 확인해 보고 싶을 때 할 수 있는 방법이 있는데 기울기의 정의를 이용하여 구하는 방법이다.
∂f/∂X 를 이용해 보자. 위의 도함수 코드를 이용하면 ∂f/∂X 값을 구할 수 있다.
이 때 X = [1, 2, 3,] 에서 X2 = [1.001, 2, 3] 를 정의하면
X2-X1 = ∂X = [0.001, 0, 0] 으로 구할 수 있고
f(X2, W) - f(X, W) = ∂f 으로 구할 수 있다. 이를 미리 구해보면
∂f = 0.99995474 - 0.9999546 = 1.35983365e-07 가 출력된다. 이를 target 이라 하겠다.
도함수 코드를 이용하여 ∂f/∂X를 출력할 수 있는데 X = [1, 2, 3]에서의 ∂f/∂X값은 1.36119358e-04이다.
여기에 ∂X를 곱해주면 ∂f를 구할 수 있다.
즉, ∂f = ∂f/∂X × ∂X 이를 pred라 하겠다.
정리하자면!!! ∂f를 구할 수 있는 방법은 2가지가 있는 것이다!
1. X2, X를 합성함수에 넣고 직접 구하기 ∂f = f(X2, W) - f(X, W) -> (target)
2. 도함수의 정의를 이용하여 구하기(pred) ∂f = ∂f(X, W)/∂X × ∂X = ∂f(X, W)/∂X × [0.001, 0, 0] -> (pred)
도함수 구하기 ~ 결과 확인까지의 파이썬 코드이다.
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[1, 2, 3]])
w = np.array([[3],
[2],
[1]])
def matmul_forward(X, W):
return np.dot(X, W)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def deriv(func, input, delta=0.001):
return (func(input + delta) - func(input)) / delta
def matrix_sigmoid(X, W, func_list):
f1 = func_list[0] # matmul
f2 = func_list[1] # sigmoid
F1 = f1(X, W)
F2 = f2(F1)
return F2
def matrix_sigmoid_deriv(X, W, func_list):
f1 = func_list[0] # matmul
f2 = func_list[1] # sigmoid
F1 = f1(X, W)
#∂(f2(f1))/∂(f1)
df2f1_df1 = deriv(f2, f1(X, W))
#∂(f1)/∂X
df1_dX = np.transpose(W, (1, 0))
#∂(f1)/∂W
df1_dW = np.transpose(X, (1, 0))
#∂(f2(f1))/∂x = ∂(f2(f1))/∂(f1) X ∂(f1)/∂x
#∂(f2(f1))/∂y = ∂(f2(f1))/∂(f1) X ∂(f1)/∂y
return df2f1_df1*df1_dX, df2f1_df1*df1_dW
list_func = [matmul_forward, sigmoid]
# do test
x2 = np.array([[1.001, 2., 3.]])
F_x2 = matrix_sigmoid(x2, w, list_func)
F_x = matrix_sigmoid(x, w, list_func)
print('f(X2, W) : ', F_x2)
print('f(X, W) : ', F_x)
dF_dX, dF_dW = matrix_sigmoid_deriv(x, w, list_func)
print('∂(f(X, W))/∂x : ', dF_dX)
target = F_x2 - F_x
pred = dF_dX[0][0] * 0.001
print('target(f(X2, W) - f(X, W) : ', target[0][0])
print('pred(∂(f(X, W))/∂x X ∂x)', pred)
결과 확인

'파이썬 프로그래밍 > 딥러닝과 수학' 카테고리의 다른 글
| 7. 2차원 행렬을 입력받는 합성함수의 도함수(실습) (0) | 2021.12.31 |
|---|---|
| 6. 2차원 행렬을 입력받는 합성함수의 도함수(이론) (0) | 2021.12.31 |
| 4. 벡터 입력에 대한 합성함수 표현 (0) | 2021.12.29 |
| 3. 입력이 여러 개인 함수와 도함수의 표현 (0) | 2021.12.28 |
| 2. 함수와 합성함수의 도함수 표현하기 (0) | 2021.12.27 |



