입력이 여러 개인 함수와 도함수는 어떻게 표현할 수 있는지 알아보자.
간단한 함수부터 출발하자.

입력 x, y를 받아서 더하여 출력한다. geogebra로 그려보면

x, y, z로 이루어진 3차원에서 2차원 평면 그래프가 그려진다.
sigmoid라고 하여 딥러닝에서 많이 봤던 함수와 합성하고자 한다.

로 정의되는 함수고,

이렇게 그려지는 함수다. 보통 classification, 분류에서 사용할 수 있는 활성화함수로도 쓰인다.
g(x) -> f(x)로 합성시킬 것이다.

이 합성함수의 그래프를 파이썬으로 그려보자. matplotlib의 3차원 모듈을 이용할 것이다.
from mpl_toolkits.mplot3d import axes3d
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
def multiple_func(x, y):
return x+y
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def comp_func(list_func, x, y):
f1 = list_func[0]
f2 = list_func[1]
return f2(f1(x, y))
func_list = [multiple_func, sigmoid]
X = np.arange(-3, 3, 0.01)
Y = np.arange(-3, 3, 0.01)
Z = comp_func(func_list, X, Y)
ax.plot(X, Y, Z, 'r', label = 'comp_func')
plt.tight_layout()
plt.legend()
plt.show()
이 합성함수의 도함수를 구할것이다. x, y에 대해 편미분 을 실시하여야 한다. 체인룰에 따라


(x, y 첨자에 유의하자)
여기서 편미분의 성질에 따라 x(또는 y)로 편미분 할 때 y(또는 x)는 상수 취급을 하므로 아래와 같이 성립한다.


위의 식을 파이썬으로 표현해 보자.
from mpl_toolkits.mplot3d import axes3d
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
def multiple_func(x, y):
return x+y
#return x*y
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def comp_func(list_func, x, y):
f1 = list_func[0]
f2 = list_func[1]
return f2(f1(x, y))
def deriv(func, input, delta=0.001):
return (func(input + delta) - func(input)) / delta
def chain_multiple_deriv_add(list_func, x, y):
f1 = list_func[0] # x + y
f2 = list_func[1] # sigmoid 1 / (1 + np.exp(-x))
#∂(f1)/∂x
df1_dx = 1
#df1_dx = y
#∂(f1)/∂y
df1_dy = 1
#df1_dy = x
#∂(f2(f1))/∂(f1)
df2f1_df1 = deriv(f2, f1(x, y))
#∂(f2(f1))/∂x = ∂(f2(f1))/∂(f1) X ∂(f1)/∂x
#∂(f2(f1))/∂y = ∂(f2(f1))/∂(f1) X ∂(f1)/∂y
return df2f1_df1*df1_dx, df2f1_df1*df1_dy
func_list = [multiple_func, sigmoid]
X = np.arange(-3, 3, 0.01)
Y = np.arange(-3, 3, 0.01)
Z = comp_func(func_list, X, Y)
ax.plot(X, Y, Z, 'r', label = 'comp_func')
Z_dx, Z_dy = chain_multiple_deriv_add(func_list, X, Y)
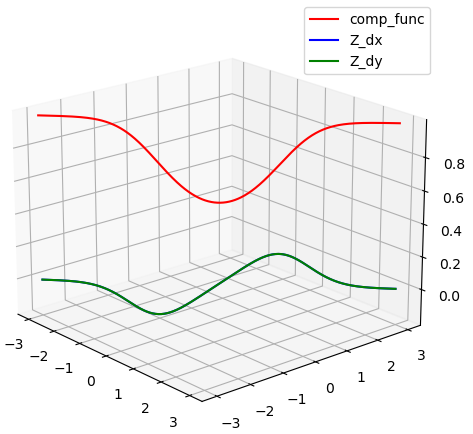
ax.plot(X, Y, Z_dx, 'b', label = 'Z_dx')
ax.plot(X, Y, Z_dy, 'g', label = 'Z_dy')
plt.tight_layout()
plt.legend()
plt.show()
그래프는 g(x,y)가 x+y일 때와 xy일때 2개를 그려보았다. xy일 때 어떻게 바뀌는지 위 코드에 주석으로 달아놓았다.

'파이썬 프로그래밍 > 딥러닝과 수학' 카테고리의 다른 글
| 6. 2차원 행렬을 입력받는 합성함수의 도함수(이론) (0) | 2021.12.31 |
|---|---|
| 5. 벡터 합성함수의 도함수 표현 (0) | 2021.12.29 |
| 4. 벡터 입력에 대한 합성함수 표현 (0) | 2021.12.29 |
| 2. 함수와 합성함수의 도함수 표현하기 (0) | 2021.12.27 |
| 1. 함수와 합성함수의 표현 (0) | 2021.12.27 |



