벡터 입력에 대한 합성함수와 도함수 표현을 알아보자.
벡터를 행렬로 표현하여 곱셈, 합성함수와 도함수를 어떻게 표현할 것인지 알아볼 것이다.
1. 벡터의 곱 연산
벡터 입력에 대해 다음과 같은 출력을 가정해 보자.(딥러닝에서 본 것 같지 않나요?)
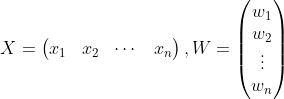

이를 파이썬 코드로 표현해보면 다음과 같다.
import numpy as np
X = np.array([[1, 2, 3]])
W = np.array([[3],
[2],
[1]])
print('x.shape', X.shape)
print('w.shape', W.shape)
def matmul_forward(X, W):
return np.dot(X, W)
print('matmul_forward ', matmul_forward(X, W))
행렬의 곱셈을 복습해보자.

이 그림이 행렬 곱셈을 가장 잘 설명한 것 같다.
'행렬'의 의미를 생각해보면 행 - 가로 , 열(렬) - 세로 를 의미한다.
행렬의 곱셈에서는 교환법칙(a×b = b×a)가 성립하지 않는다. 다시 말해 행렬에서는 (a×b ≠ b×a)이다.
곱셈 순서이다.
1. A행렬의 열, B행렬의 행의 수가 일치하는지 확인해야 한다.
-> A(m×k) × B(k×n) 으로 일치한다.
2. A행렬의 행, B행렬의 열이 곱셈 행렬의 행렬이 된다.
-> A(m×k) × B(k×n) = AB(m×n)
즉, 일치하는 수를 '소거' 시키면서 곱셈해주고 나머지를 앞뒤로 결합하는 느낌으로 계산한다.
결과는 다음과 같다.
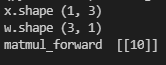
X(1, 3) × W(3, 1) = XW(1, 1) 의 행렬이 계산되었고 실제 계산해 보면 1×3 + 2×2 + 3×1 = 10 이다.
2. 벡터함수와 합성함수
벡터함수를 sigmoid 함수에 통과하는 합성함수( f(X, W) )를 정의할 것이다.
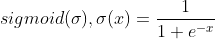

파이썬 코드로 표현하면 다음과 같다.
import numpy as np
x = np.array([[1, 2, 3]])
w = np.array([[3],
[2],
[1]])
def matmul_forward(X, W):
return np.dot(X, W)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def matrix_sigmoid(X, W, func_list):
f1 = func_list[0] # matmul
f2 = func_list[1] # sigmoid
F1 = f1(X, W)
F2 = f2(F1)
return F2
list_func = [matmul_forward, sigmoid]
print('matrix_sigmoid', matrix_sigmoid(x, w, list_func))결과를 출력하면 [[0.9999546]] 이다.

sigmoid 함수는
x가 양의 값일 때 1에 수렴
x = 0일 때 0.5,
x가 음의 값일 때 0에 수렴
따라서 sigmoid(10) 값은 1에 가까워진다. 즉 출력 결과는 합당하다고 볼 수 있다.
'파이썬 프로그래밍 > 딥러닝과 수학' 카테고리의 다른 글
| 6. 2차원 행렬을 입력받는 합성함수의 도함수(이론) (0) | 2021.12.31 |
|---|---|
| 5. 벡터 합성함수의 도함수 표현 (0) | 2021.12.29 |
| 3. 입력이 여러 개인 함수와 도함수의 표현 (0) | 2021.12.28 |
| 2. 함수와 합성함수의 도함수 표현하기 (0) | 2021.12.27 |
| 1. 함수와 합성함수의 표현 (0) | 2021.12.27 |



