6. 2차원 행렬을 입력받는 합성함수의 도함수(이론)

1. 2차원 행렬을 입력받는 합성함수의 정의

 

입력이 2차원인 경우에는 도함수를 어떻게 구할 수 있을까? 일단 합성함수부터 정의하자.

입력 X, W는 아래와 같다. 

X.shape (3, 3) , W.shape(3, 2)

 

g(X, W)함수를 아래와 같이 정의한다.

g(X, W) = X × W shape (3, 2)

간략하게 표기한 g(X, W)

σ(X) 함수를 아래와 같이 정의한다.

σ 시그마, 시그모이드 함수

 

h(X) 함수를 아래와 같이 정의한다.

각 요소들의 합

 

합성함수 f(X, W) = h(σ(g(X, W)))를 정의한다. 합성함수의 정의와 연산의 결과는 아래와 같다.

합성함수의 정의

합성함수 연산 결과

 

딥러닝에서 상당히 유사하게 사용하는 forward 연산이다. g -> σ -> h 정방향 순서대로 연산하여 출력한다.

 

 

 

2. 도함수 구하기

 

도함수는 체인룰을 사용하여 forward 연산과 반대로 h -> σ -> g 순서대로 구한다. 그래서 backward 연산이다. 

우리는 X의 변화에 따른 최종출력 f의 변화가 궁금한 것인데 바로 알 수 없기 때문이다. 따라서

 

1) σ 변화에 따른 h의 변화

 

 

2) g에 따른 σ의 변화

 

 

 

3) X에 따른 g의 변화

 

 

이렇게 역으로 변화율을 알아가면 입력 X에 따른 최종출력 f의 변화를 알 수 있는 것이다. 이를 수식으로 표현하면

 

여기서부터 머리가 아파진다. 잘 따라 오세요.

 

1)σ 변화에 따른 h의 변화

 

 

2) g에 따른 σ의 변화

 

3) X에 따른 g의 변화(왜 이렇게 연산하는지 명확히 이해하지 못했지만 이렇게 연산한다고 한다...)

 

따라서 ∂f/∂X 는 아래와 같이 성립한다.

(1로 이루어진 행렬은 shape이 같은 ∂σ/∂g와 이동하여 요소 곱이 된다.-> 이것도 명확히 이해가...)

 

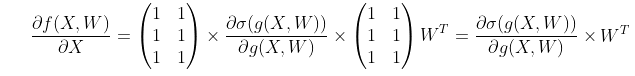
∂f/∂W 는 위의 연산을 응용하다 보면 아래와 같이 나온다.

 

 

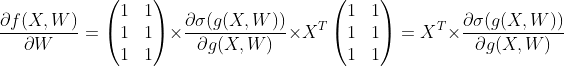
이렇게 하여 도함수를 다 구한 것이다.

다음에는 파이썬 코드로 알아보고 pytorch로 정말 맞는지 검산해 볼 것이다.