저번 시간까지 다층 퍼셉트론(Multi-Layer Perceptron, MLP)을 이용하여 학습을 시켜보았다.
정의에 대해 조금 더 이야기를 해 보자면
일반적으로 MLP는 고전적인, 완전 연결 신경망으로 볼 수 있는데
'일반적으로' 3개의 층에 sigmoid, tanh의 활성화 함수를 가진 신경망을 이야기한다.
(본인의 예제에서 활성화 함수를 relu를 사용하였지만...)
여기서 DNN은 더 확장하여 순환(RNN, LSTM)을 할 수 있다던지, 완전 연결이 아니라던지, 활성화 함수가 0 또는 1이 아니라던지 등등 더욱 포괄적이고 상위적인 개념이 포함된다. 단순히 은닉 층 개수로 나눌 수는 없다.
제목은 DNN으로 거창하게 하였지만, 사실 MLP는 DNN의 하위개념이므로(...) 구현 상 큰 차이가 없다. DNN과 MLP의 차이는 무엇이냐에 대해 사실 많은 언쟁이 오간다. (https://stats.stackexchange.com/questions/315402/multi-layer-perceptron-vs-deep-neural-network) 참고해 보길 바란다.
이번 예제에서는 이전시간 MLP로 구현했던 콘크리트 강도 예측하기(https://toyourlight.tistory.com/38)를 히든 레이어 1개를 더 추가하여 2개의 히든 레이어로 학습하는 DNN으로 표현해 볼 것이다.
구현 과정은 MLP 포스트를 참고해 보는 것이 좋다.
(17. 다층 퍼셉트론(MPL)의 등장-2.비선형 회귀식(심화이론))
(18. 다층 퍼셉트론(MPL)의 등장-2.비선형 회귀식(실습))
1. 전처리 하기
데이터 전처리하기(https://toyourlight.tistory.com/38)를 참고해 보자. 표준화(Standardization) 해준다.
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
np.random.seed(20220214)
data = genfromtxt('ConcreteStrengthData.csv', delimiter=',', skip_header = 1)
norm_data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
2. 초기화 및 가중치 설정
데이터 셋을 훈련 세트와 테스트 세트로 분류한다. 1000개를 훈련 세트, 마지막 30개를 테스트 세트로 할 것이다.
train_data = norm_data[:1000, :]
test_data = norm_data[1000:, :]
inputs = train_data[:, 0:8]
targets = train_data[:, -1:]
test_inputs = test_data[:, 0:8]
test_targets = test_data[:, -1:]
콘크리트 강도 예측하기 데이터셋의 특성(feature)는 8개임을 기억하자. 그렇다면 입력, 가중치, 편향 및 출력 shape은 아래와 같다.

다이어그램을 그리면 아래와 같다.

구현 코드이다.
W1 = np.random.randn(8, 8)
B1 = np.random.randn(8, 1)
W2 = np.random.randn(8, 8)
B2 = np.random.randn(8, 1)
W3 = np.random.randn(8, 8)
B3 = np.random.randn(8, 1)
W4 = np.random.randn(1, 8)
B4 = np.random.randn(1, 1)
learning_rate = 0.001
batch_size = 256
steps=0
epochs = 3000
만약 다른 노드 개수로 하고 싶으면 아래와 같이 구성봐도 나쁘지 않을 것이다. (그렇다면 learning_rate, batch_size, epochs 같은 Hyperparameter도 바뀌어야 한다.)

W1 = np.random.randn(32, 8)
B1 = np.random.randn(32, 1)
W2 = np.random.randn(16, 32)
B2 = np.random.randn(16, 1)
W3 = np.random.randn(8, 16)
B3 = np.random.randn(8, 1)
W4 = np.random.randn(1, 8)
B4 = np.random.randn(1, 1)
3. 순전파(forward) 정의
순전파를 정의한다. 순전파 함수에는 아래와 같은 순서도 진행되며 오차도 계산한다.
G연산과 R 연산은 위의 포스트를 참고하길 바란다.

오차함수(Loss function)는 MSE를 이용한다.
def forward(input, target):
X = np.transpose(input, (1, 0)) # (8, batch)
G1 = np.dot(W1, X) + B1 #(8, batch)
R1 = np.maximum(0, G1) #(8, batch)
G2 = np.dot(W2, R1) + B2 #(8, batch)
R2 = np.maximum(0, G2) #(8, batch)
G3 = np.dot(W3, R2) + B3 #(8, batch)
R3 = np.maximum(0, G3) #(8, batch)
G4 = np.dot(W4, R3) + B4 # (1, batch) -> pred
pred = np.transpose(G4, (1, 0))
loss = np.mean(np.power((pred-target), 2))
return G1, R1, G2, R2, G3, R3, G4, pred, loss
4. 역전파(backward)
MLP에서 히든 레이어가 1개만 더 추가된 경우이므로 가장 깊은 곳의 가중치와 편향인 W1, B1을 구해보겠다.
그 외의 내용은 위 포스트를 참고하시라. MLP와 큰 차이가 없다.
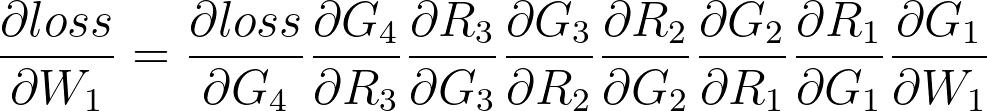

구현 방법은 MLP 포스트를 참고해 보자. 각 변수에 대한 도함수를 정의하고, 연쇄법칙(Chain rule)을 이용하여 오차에 대한 가중치와 편향의 도함수를 구하는 방법이다.
def backward(input, target, G1, R1, G2, R2, G3, R3, G4):
target = np.transpose(target, (1, 0)) # (1, batch)
dL_dG4 = 2*(G4-target) / len(target[0]) # (1, batch)
dG4_dW4 = np.transpose(R3, (1, 0)) # (batch, 8)
dG4_dB4 = np.ones_like(B4) # (1, batch)
dG4_dR3 = np.transpose(W4, (1, 0)) # (8, 1)
dR3_dG3 = np.where(R3>0, 1, 0) # (8, batch)
dG3_dW3 = np.transpose(R2, (1, 0)) # (batch, 8)
dG3_dB3 = np.ones_like(B3) # (8, batch)
dG3_dR2 = np.transpose(W3, (1, 0)) # (8, 8)
dR2_dG2 = np.where(R2>0, 1, 0) # (8, batch)
dG2_dW2 = np.transpose(R1, (1, 0)) # (batch, 8)
dG2_dB2 = np.ones_like(B2) # (8, batch)
dG2_dR1 = np.transpose(W2, (1, 0)) # (8, 8)
dR1_dG1 = np.where(R1>0, 1, 0) # (8, batch)
dG1_dW1 = input # (batch, 8)
dG1_dB1 = np.ones_like(B1) # (8, batch)
#chain rule
#operation W4, B4
dL_dW4 = np.dot(dL_dG4, dG4_dW4) # (1, 8)
dL_dB4 = np.sum(dL_dG4*dG4_dB4, keepdims=True) # (1, 1)
#operation W3, B3
dL_dG3 = np.dot(dG4_dR3, dL_dG4) * dR3_dG3
dL_dW3 = np.dot(dL_dG3, dG3_dW3) # (8, 8)
dL_dB3 = np.sum(dL_dG3*dG3_dB3, axis=1, keepdims=True) # (8, 1)
#operation W2, B2
dL_dG2 = np.dot(dG3_dR2, dL_dG3) * dR2_dG2
dL_dW2 = np.dot(dL_dG2, dG2_dW2) # (8, 8)
dL_dB2 = np.sum(dL_dG2*dG2_dB2, axis=1, keepdims=True) # (8, 1)
#operation W1, B1
dL_dG1 = np.dot(dG2_dR1, dL_dG2) * dR1_dG1
dL_dW1 = np.dot(dL_dG1, dG1_dW1) # (8, 8)
dL_dB1 = np.sum(dL_dG1*dG1_dB1, axis=1, keepdims=True) # (8, 1)
return dL_dW1, dL_dB1, dL_dW2, dL_dB2, dL_dW3, dL_dB3, dL_dW4, dL_dB4
결과는 어떻게 되었을까?
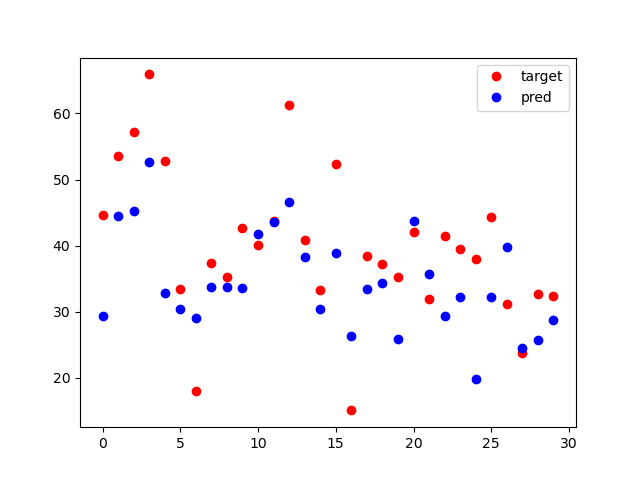
너무 큰 기대를 했을까? MLP랑 큰 차이가 없는 듯 하다. 사실 당연한 이유인게, 안정성이 매우 뒤떨어지는 날것 그대로의 코드이기 때문이다.
아래는 전체 코드이다.
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
np.random.seed(20220214)
data = genfromtxt('ConcreteStrengthData.csv', delimiter=',', skip_header = 1)
norm_data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
train_data = norm_data[:1000, :]
test_data = norm_data[1000:, :]
inputs = train_data[:, 0:8]
targets = train_data[:, -1:]
test_inputs = test_data[:, 0:8]
test_targets = test_data[:, -1:]
W1 = np.random.randn(8, 8)
B1 = np.random.randn(8, 1)
W2 = np.random.randn(8, 8)
B2 = np.random.randn(8, 1)
W3 = np.random.randn(8, 8)
B3 = np.random.randn(8, 1)
W4 = np.random.randn(1, 8)
B4 = np.random.randn(1, 1)
learning_rate = 0.001
batch_size = 256
steps=0
epochs = 3000
def make_batch(input, target, step, batch_size):
if len(input) >= step + batch_size:
input_batch = input[step : step + batch_size]
target_batch = target[step : step + batch_size]
else:
input_batch = input[step : ]
target_batch = target[step : ]
return input_batch, target_batch
def forward(input, target):
X = np.transpose(input, (1, 0)) # (8, batch)
G1 = np.dot(W1, X) + B1 #(8, batch)
R1 = np.maximum(0, G1) #(8, batch)
G2 = np.dot(W2, R1) + B2 #(8, batch)
R2 = np.maximum(0, G2) #(8, batch)
G3 = np.dot(W3, R2) + B3 #(8, batch)
R3 = np.maximum(0, G3) #(8, batch)
G4 = np.dot(W4, R3) + B4 # (1, batch) -> pred
pred = np.transpose(G4, (1, 0))
loss = np.mean(np.power((pred-target), 2))
return G1, R1, G2, R2, G3, R3, G4, pred, loss
def backward(input, target, G1, R1, G2, R2, G3, R3, G4):
target = np.transpose(target, (1, 0)) # (1, batch)
dL_dG4 = 2*(G4-target) / len(target[0]) # (1, batch)
dG4_dW4 = np.transpose(R3, (1, 0)) # (batch, 8)
dG4_dB4 = np.ones_like(B4) # (1, batch)
dG4_dR3 = np.transpose(W4, (1, 0)) # (8, 1)
dR3_dG3 = np.where(R3>0, 1, 0) # (8, batch)
dG3_dW3 = np.transpose(R2, (1, 0)) # (batch, 64)
dG3_dB3 = np.ones_like(B3) # (8, batch)
dG3_dR2 = np.transpose(W3, (1, 0)) # (8, 8)
dR2_dG2 = np.where(R2>0, 1, 0) # (8, batch)
dG2_dW2 = np.transpose(R1, (1, 0)) # (batch, 8)
dG2_dB2 = np.ones_like(B2) # (8, batch)
dG2_dR1 = np.transpose(W2, (1, 0)) # (8, 8)
dR1_dG1 = np.where(R1>0, 1, 0) # (8, batch)
dG1_dW1 = input # (batch, 8)
dG1_dB1 = np.ones_like(B1) # (8, batch)
#chain rule
#operation W4, B4
dL_dW4 = np.dot(dL_dG4, dG4_dW4) # (1, 8)
dL_dB4 = np.sum(dL_dG4*dG4_dB4, keepdims=True) # (1, 1)
#operation W3, B3
dL_dG3 = np.dot(dG4_dR3, dL_dG4) * dR3_dG3
dL_dW3 = np.dot(dL_dG3, dG3_dW3) # (8, 8)
dL_dB3 = np.sum(dL_dG3*dG3_dB3, axis=1, keepdims=True) # (8, 1)
#operation W2, B2
dL_dG2 = np.dot(dG3_dR2, dL_dG3) * dR2_dG2
dL_dW2 = np.dot(dL_dG2, dG2_dW2) # (8, 8)
dL_dB2 = np.sum(dL_dG2*dG2_dB2, axis=1, keepdims=True) # (8, 1)
#operation W1, B1
dL_dG1 = np.dot(dG2_dR1, dL_dG2) * dR1_dG1
dL_dW1 = np.dot(dL_dG1, dG1_dW1) # (8, 8)
dL_dB1 = np.sum(dL_dG1*dG1_dB1, axis=1, keepdims=True) # (8, 1)
return dL_dW1, dL_dB1, dL_dW2, dL_dB2, dL_dW3, dL_dB3, dL_dW4, dL_dB4
_, _, _, _, _, _, _, pred, loss = forward(inputs, targets)
print('before loss', loss)
arr_loss = []
for i in range(2000):
while steps <= len(inputs):
x_batch, y_batch = make_batch(inputs, targets, steps, batch_size)
G1, R1, G2, R2, G3, R3, G4, _, loss = forward(x_batch, y_batch)
dL_dW1, dL_dB1, dL_dW2, dL_dB2, dL_dW3, dL_dB3, dL_dW4, dL_dB4 \
= backward(x_batch, y_batch, G1, R1, G2, R2, G3, R3, G4)
W1 = W1 + -1*learning_rate * dL_dW1
B1 = B1 + -1*learning_rate * dL_dB1
W2 = W2 + -1*learning_rate * dL_dW2
B2 = B2 + -1*learning_rate * dL_dB2
W3 = W3 + -1*learning_rate * dL_dW3
B3 = B3 + -1*learning_rate * dL_dB3
W4 = W4 + -1*learning_rate * dL_dW4
B4 = B4 + -1*learning_rate * dL_dB4
arr_loss.append(loss)
steps += batch_size
if steps > len(inputs):
steps = 0
np.random.shuffle(train_data)
break
_, _, _, _, _, _, _, pred, loss = forward(inputs, targets)
print('after loss', loss)
_, _, _, _, _, _, _, pred, test_loss = forward(test_inputs, test_targets)
print('test loss', test_loss)
norm_data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
# 역정규화, 정규화의 연산을 다시 풀어준다. data[:, -1:] 는 마지막 target 값을 의미한다.
test_targets = test_targets * np.std(data[:, -1:], axis=0) + np.mean(data[:, -1:], axis=0)
pred = pred * np.std(data[:, -1:], axis=0) + np.mean(data[:, -1:], axis=0)
plt.plot(test_targets, 'ro', label='target')
plt.plot(pred, 'bo', label='pred')
#plt.xlabel('arry', size=15)
#plt.ylabel('value', size=15)
plt.legend()
#plt.plot(arr_loss)
plt.show()
5. Pytorch로 실행해 본다면?
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from numpy import genfromtxt
import numpy as np
import matplotlib.pyplot as plt
torch.manual_seed(220214)
data = genfromtxt('ConcreteStrengthData.csv', delimiter=',', skip_header = 1)
norm_data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
train_data = torch.FloatTensor(norm_data[:1000, :])
test_data = torch.FloatTensor(norm_data[1000:, :])
inputs = train_data[:, 0:8]
targets = train_data[:, -1:]
test_inputs = test_data[:, 0:8]
test_targets = test_data[:, -1:]
model = nn.Sequential(
nn.Linear(8, 8),
nn.ReLU(),
nn.Linear(8, 8),
nn.ReLU(),
nn.Linear(8, 8),
nn.ReLU(),
nn.Linear(8, 1),
)
pred = model(inputs)
loss = F.mse_loss(pred, targets)
print('before loss', loss)
optimizer = optim.SGD(model.parameters(), lr=0.15)
epoches = 3000
for epoche in range(epoches + 1):
pred = model(inputs)
loss = F.mse_loss(pred, targets)
optimizer.zero_grad()
loss.backward()
optimizer.step()
pred = model(inputs)
loss = F.mse_loss(pred, targets)
print('after loss', loss)
test_pred = model(test_inputs)
test_targets = test_targets * np.std(data[:, -1:], axis=0) + np.mean(data[:, -1:], axis=0)
test_pred = test_pred.detach() * np.std(data[:, -1:], axis=0) + np.mean(data[:, -1:], axis=0)
plt.plot(test_targets, 'ro', label='target')
plt.plot(test_pred, 'bo', label='pred')
plt.legend()
plt.show()

Numpy DNN과 Pytorch DNN과 큰 차이가 없는 것 같다. 그런데, 일반적인 딥러닝 라이브러리는 손으로 짜는 것 보다 어마어마한 안정성을 자랑한다. 만약 가중치를 바꾸어 보면 어떻게 될까? 가중치와 학습률을 아래와 같이 바꾸어보자.
model = nn.Sequential(
nn.Linear(8, 256),
nn.ReLU(),
nn.Linear(256, 64),
nn.ReLU(),
nn.Linear(64, 8),
nn.ReLU(),
nn.Linear(8, 1),
)
optimizer = optim.SGD(model.parameters(), lr=0.2)
결과는?

이래서 딥러닝 라이브러리를 쓰는 것이다. 위 가중치를 Numpy로 한다면 최적화 때문에 시간도 오래 걸리기도 하고 안정성이 낮아 overflow가 나기 쉽다.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 27. [CNN기초] 1차원 배열 CNN 훈련하기-1 (0) | 2023.01.03 |
|---|---|
| 26. [CNN기초] CNN 개요 (0) | 2023.01.01 |
| 24. 딥러닝에서 데이터 표준화, 정규화가 필요한 이유 (0) | 2022.04.19 |
| 23 - 학습 성능 개선 : Mini batch & Shuffle 구현하기 (0) | 2022.02.11 |
| 22. 다중회귀-소프트맥스 함수 역전파(고급, 쉬운 방법) (0) | 2022.02.10 |



