딥러닝 실행 전에 데이터 표준화(Normalization)와 정규화(Standardization)가 왜 필요할까?
Kaggle 콘크리트 강도 계산(Calculate Concrete Strength) 데이터를 예시로 들어보자.
콘크리트 강도 계산 feature는 8개로 구성되어 있는데 각각 성질은 아래와 같다.
- Cement Component : - 시멘트의 혼합량
- Blast Furnace Slag : - 고로 슬래그 미분말 함유량 (링크 참고)
- Fly Ash Component : - 플라이애시 혼합량(링크 참고)
- Water Component : - 물 혼합량
- Superplasticizer Component : - 가소제 혼합량(링크 참고)
- Coarse Aggregate Component : - 굵은 골재 함유량
- Fine Aggregate Component : - 잔 골재 함유량
- Age In Days : 건조 상태로 남아 있던 날 수
- Strength(Target) :- 콘크리트의 최종 강도는 무엇이었습니까- (목표)
먼저 데이터가 어떻게 분포 되어있는지 확인해 봐야한다. Pandas와 Seaborn을 이용해 몇줄만으로 차트를 그릴 수 있지만, 추가 라이브러리 없이 Numpy와 Matplotlib만 이용해 보겠다.
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
data = genfromtxt('ConcreteStrengthData.csv', delimiter=',', skip_header = 1)
fig, ax = plt.subplots(2, 5)
ax[0][0].plot(data[:, 0])
ax[0][0].set_title('CementComponent', fontsize=10)
ax[0][1].plot(data[:, 1])
ax[0][1].set_title('BlastFurnaceSlag', fontsize=10)
ax[0][2].plot(data[:, 2])
ax[0][2].set_title('FlyAshComponent', fontsize=10)
ax[0][3].plot(data[:, 3])
ax[0][3].set_title('WaterComponent', fontsize=10)
ax[1][0].plot(data[:, 4])
ax[1][0].set_title('SuperplasticizerComponent', fontsize=10)
ax[1][1].plot(data[:, 5])
ax[1][1].set_title('CoarseAggregateComponent', fontsize=10)
ax[1][2].plot(data[:, 6])
ax[1][2].set_title('FineAggregateComponent', fontsize=10)
ax[1][3].plot(data[:, 7])
ax[1][3].set_title('AgeInDays', fontsize=10)
ax[1][4].plot(data[:, 8])
ax[1][4].set_title('Strength', fontsize=10)
plt.show()

마지막 Strength가 콘크리트 굳기로 목표값이다.
각 요소별 데이터값들의 그래프를 그려보았는데 값들의 범위가 너무 천차만별이다.
이렇게 값들의 범위가 다르면 제대로 훈련할 수 없다.
제대로 훈련하기 위해 정규화와 표준화가 필요한 이유다.
예를 들어 첫번째 시멘트 함류량(Cement component)에서 100 수치는 작은 값이지만 그 아래 그래프인 가소제 함유량(Superplasticizer)에서는 엄청나게 많은 양이다.
이 데이터를 기준을 세우고 통일 시켜야 한다.
이 글 에서도 나와있지만 여러가지 기준을 세우는 방법이 있다. 본인은 일반적으로 3가지 방법을 사용한다.
Zscore가 만능이 아니다. 훈련만 잘 되면 그만 아닌가?
1. 데이터 수를 작게 만들기 → 소수점 곱해주기
데이터에 일정한 소수 (Ex : 0.001)을 곱하여 데이터 자체를 작게 만드는 방법이다. 이렇게 하면 곱하지 않을 때 보다 데이터가 훨씬 안정적으로 인식하고 계산할 수 있게 된다. 본인은 가장 첫 번째로 이 방법을 사용한다.
data = genfromtxt('ConcreteStrengthData.csv', delimiter=',', skip_header = 1)
train_data = data[:1000, :]*0.001
test_data = data[1000:, :]*0.001
각 데이터에 0.001을 곱하고 1030개 데이터중 1000개를 Train Data, 30개를 Test Data로 만든 것이다.
훈련을 마치고 그래프로 그려 확인해 보기 위해 다시 1000을 곱해 주어야 한다.
_, _, _, _, _, pred, test_loss = forward(test_inputs, test_targets, W1, B1, W2, B2, W3, B3)
print('test loss', test_loss)
plt.plot(test_targets*1000, 'ro', label='target')
plt.plot(pred*1000, 'bo', label='pred')
plt.legend()
plt.show()
아래는 훈련 결과이다.
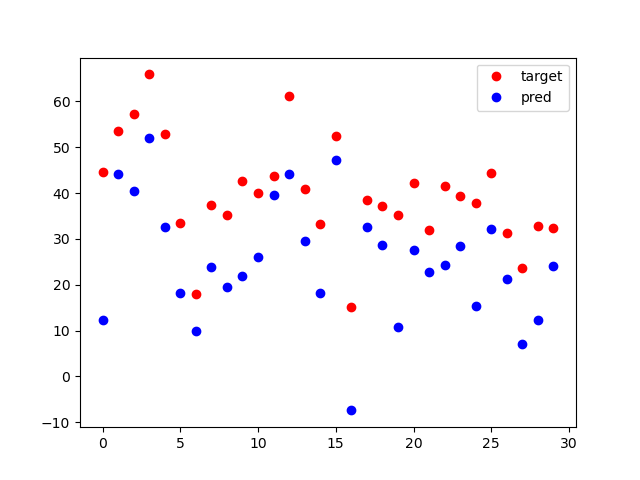
파란색점이 MPL로 구성하고 훈련한 모델이 예측(pred)한 결과이고
빨간색 점이 실제 값(Target)이다. 오차값은 각 그래프 값의 수직값을 봐야 한다. 수직으로 겹칠 수록 오차가 작은 것이다.
2. 정규화(Normalization)
데이터를 정규화 시켜보자. 정규화 방법은 여기 를 참고하면 된다.
norm_data = (data - data.min(axis=0)) \
/ (data.max(axis=0) - data.min(axis=0))
훈련이 끝나고 결과를 확인하기 위해 역정규화를 해주어야 한다.
# 역정규화, 정규화의 연산을 다시 풀어준다. data[:, -1:] 는 마지막 target 값을 의미한다.
test_targets = test_targets * (data[:, -1:].max(axis=0) - data[:, -1:].min(axis=0)) + data[:, -1:].min(axis=0)
pred = pred * (data[:, -1:].max(axis=0) - data[:, -1:].min(axis=0)) + data[:, -1:].min(axis=0)
print('test loss', test_loss)
plt.plot(test_targets, 'ro', label='target')
plt.plot(pred, 'bo', label='pred')
plt.legend()
plt.show()
결과는?
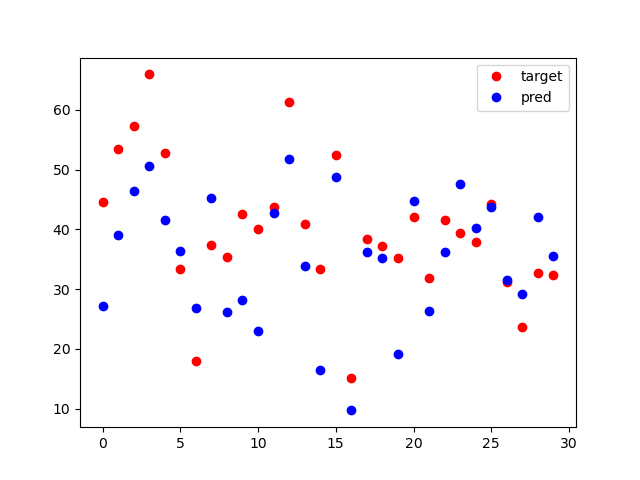
결과가 드라마틱하게 변할 수도 있고 아닐 수도 있다. 아니라고 해서 큰 실망 마시길 바란다.
3. 표준화(Standarization)
가장 많이 사용하는 표준화를 할 것이다. 표준화 방법은 여기 를 참고하길 바란다.
표준화는 마지막에 MPL 풀 코드를 제시하겠다. 아래는 데이터의 표준화이다.
norm_data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
훈련 후 마지막에 역 표준화를 해 주어야 한다.
# 역표준화, 표준화의 연산을 다시 풀어준다. data[:, -1:] 는 마지막 target 값을 의미한다.
test_targets = test_targets * np.std(data[:, -1:], axis=0) + np.mean(data[:, -1:], axis=0)
pred = pred * np.std(data[:, -1:], axis=0) + np.mean(data[:, -1:], axis=0)
plt.plot(test_targets, 'ro', label='target')
plt.plot(pred, 'bo', label='pred')
plt.legend()
plt.show()
결과는?

드라마틱한 결과는 크게 하지 마시오(...)
아래는 표준화 중 Zscore를 이용한 MPL 코드이다.
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
"""
Setup Hyperparameters
np.random.seed(20220214)
W1 = np.random.randn(32, 8)
B1 = np.random.randn(32, 1)
W2 = np.random.randn(8, 32)
B2 = np.random.randn(8, 1)
W3 = np.random.randn(1, 8)
B3 = np.random.randn(1, 1)
learning_rate = 0.004
batch_size = 500
steps=0
epochs = 3000
before loss 417.82988286417947
before loss 0.24167556631433623
test loss 0.2483900751894638
"""
data = genfromtxt('ConcreteStrengthData.csv', delimiter=',', skip_header = 1)
norm_data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
train_data = norm_data[:1000, :]
test_data = norm_data[1000:, :]
inputs = train_data[:, 0:8]
targets = train_data[:, -1:]
test_inputs = test_data[:, 0:8]
test_targets = test_data[:, -1:]
np.random.seed(20220214)
W1 = np.random.randn(32, 8)
B1 = np.random.randn(32, 1)
W2 = np.random.randn(8, 32)
B2 = np.random.randn(8, 1)
W3 = np.random.randn(1, 8)
B3 = np.random.randn(1, 1)
learning_rate = 0.004
batch_size = 500
steps=0
epochs = 3000
def make_batch(input, target, step, batch_size):
if len(input) >= step + batch_size:
input_batch = input[step : step + batch_size]
target_batch = target[step : step + batch_size]
else:
input_batch = input[step : ]
target_batch = target[step : ]
return input_batch, target_batch
def forward(input, target, W1, B1, W2, B2, W3, B3):
#G1 operation
X = np.transpose(input, (1, 0)) # (1, batch)
G1 = np.dot(W1, X) + B1 # (8, batch)
R1 = np.maximum(0, G1) # (8, batch)
G2 = np.dot(W2, R1) + B2 # (4, batch)
R2 = np.maximum(0, G2) # (4, batch)
G3 = np.dot(W3, R2) + B3 # (1, batch)
pred = np.transpose(G3, (1, 0)) # (batch, 1)
loss = np.mean(np.power(pred-target, 2)) #(1, 1)
return G1, R1, G2, R2, G3, pred, loss
def loss_gradient(input, target, W1, B1, W2, B2, W3, B3):
G1, R1, G2, R2, G3, _, _ = forward(input, target, W1, B1, W2, B2, W3, B3)
target = np.transpose(target, (1, 0)) # (1, batch)
dL_dG3 = 2*(G3-target) / len(target[0]) # (1, batch)
dG3_dR2 = np.transpose(W3, (1, 0)) # (4, 1)
dG3_dW3 = np.transpose(R2, (1, 0)) # (batch, 4)
dG3_dB3 = np.ones_like(B3) # (1, 1)
dR2_dG2 = np.where(R2>0, 1, 0) # (4, batch)
dG2_dR1 = np.transpose(W2, (1, 0)) # (8, 4)
dG2_dW2 = np.transpose(R1, (1, 0)) # (batch, 8)
dG2_dB2 = np.ones_like(B2) # (4, 1)
dR1_dG1 = np.where(R1>0, 1, 0) # (8, batch)
dG1_dW1 = input # (batch, 1) 왜냐면 input의 전치가 연산되었는데 다시 전치하므로 원래 모양이 됨.
dG1_dB1 = np.ones_like(B3) # (8, 1)
# chain rule
# operation W3, B3
dL_dW3 = np.dot(dL_dG3, dG3_dW3) # (1, 4)
dL_dB3 = np.sum(dL_dG3, keepdims=True) * dG3_dB3 # (1, 1)
# operation W2, B2
dL_dG2 = np.dot(dG3_dR2, dL_dG3) * dR2_dG2 # (4, batch)
dL_dW2 = np.dot(dL_dG2, dG2_dW2) # (4, 8)
dL_dB2 = np.sum(dL_dG2, axis = 1, keepdims=True) * dG2_dB2 # (4, 1)
# operation W1, B1
dL_dG1 = np.dot(dG2_dR1, dL_dG2) * dR1_dG1 # (8, batch)
dL_dW1 = np.dot(dL_dG1, dG1_dW1) # (8, 1)
dL_dB1 = np.sum(dL_dG1, axis=1, keepdims=True) * dG1_dB1 # (8, 1)
return dL_dW1, dL_dB1, dL_dW2, dL_dB2, dL_dW3, dL_dB3
_, _, _, _, _, pred, loss = forward(inputs, targets, W1, B1, W2, B2, W3, B3)
#print('before pred', pred)
print('before loss', loss)
arr_loss = []
for i in range(epochs):
while steps <= len(inputs):
x_batch, y_batch = make_batch(inputs, targets, steps, batch_size)
_, _, _, _, _, _, loss = forward(x_batch, y_batch, W1, B1, W2, B2, W3, B3)
dL_dW1, dL_dB1, dL_dW2, dL_dB2, dL_dW3, dL_dB3 = loss_gradient(x_batch, y_batch, W1, B1, W2, B2, W3, B3)
W1 = W1 + -1*learning_rate * dL_dW1
B1 = B1 + -1*learning_rate * dL_dB1
W2 = W2 + -1*learning_rate * dL_dW2
B2 = B2 + -1*learning_rate * dL_dB2
W3 = W3 + -1*learning_rate * dL_dW3
B3 = B3 + -1*learning_rate * dL_dB3
arr_loss.append(loss)
steps += batch_size
if steps > len(inputs):
steps = 0
np.random.shuffle(train_data)
break
_, _, _, _, _, pred, loss = forward(inputs, targets, W1, B1, W2, B2, W3, B3)
#print('before pred', pred)
print('after loss', loss)
_, _, _, _, _, pred, test_loss = forward(test_inputs, test_targets, W1, B1, W2, B2, W3, B3)
print('test loss', test_loss)
# 역표준화, 표준화의 연산을 다시 풀어준다. data[:, -1:] 는 마지막 target 값을 의미한다.
test_targets = test_targets * np.std(data[:, -1:], axis=0) + np.mean(data[:, -1:], axis=0)
pred = pred * np.std(data[:, -1:], axis=0) + np.mean(data[:, -1:], axis=0)
plt.plot(test_targets, 'ro', label='target')
plt.plot(pred, 'bo', label='pred')
#plt.xlabel('arry', size=15)
#plt.ylabel('value', size=15)
plt.legend()
#plt.plot(arr_loss)
plt.show()각 Hyperparameter를 변경해 보고 결과를 각각 확인해 보자.
4. 전처리를 안한다면?
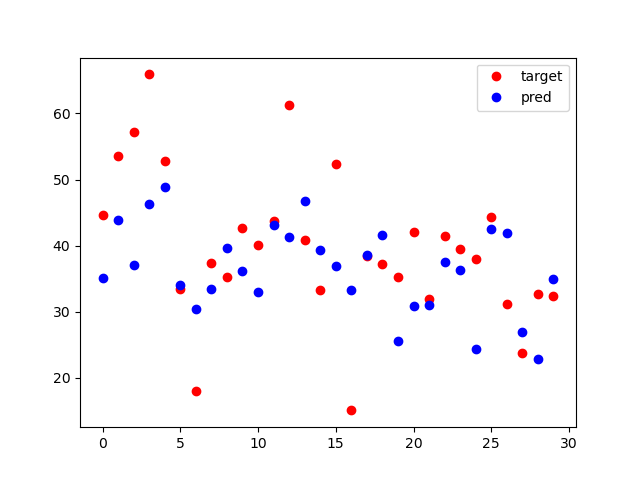
이 데이터는 MPL에서는 다행이도 전처리에 큰 영향을 안 받는것 같기도 한데 전체 오타는 전처리보다 확실히 크다.
(전처리 안하면 평균 오차 9이고, 전처리를 하면 오차가 소수점으로 나온다)
그래서 순서는
전처리 하지 않고 훈련해 보고 이건 아니다 싶으면
1 (소수점 곱하기)
→ 2 (정규화 Normalization)
→ 3 (표준화 Stardarization) 순서대로 전처리
해 보고 결과를 확인 후 가장 괜찮은 전처리 방법을 사용하자.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 26. [CNN기초] CNN 개요 (0) | 2023.01.01 |
|---|---|
| 25 - Deep Neural Nets 구현하기 (0) | 2022.04.20 |
| 23 - 학습 성능 개선 : Mini batch & Shuffle 구현하기 (0) | 2022.02.11 |
| 22. 다중회귀-소프트맥스 함수 역전파(고급, 쉬운 방법) (0) | 2022.02.10 |
| 21. 경사하강법의 개선 - Adam (0) | 2022.02.05 |



