지난 시간까지 복잡한 데이터에 대한 학습은 다중 퍼셉트론(MLP)가 효율적이라는 것을 배웠고 좀 더 빠르게 수렴하기 위해 경사하강법을 Momentum, RMSprop, Adam 으로 개선하여 학습해 보았다.
이번 시간부터 '학습 성능 개선'을 주제로 어떻게 해야 좀 더 빠르고 효율적으로 학습을 할 수 있을가에 대해 여러 방법들을 알아볼 것이다. 학습 성능을 개선한다는 것은 최단 학습으로 지역 최소점에 빠지지 않고 전역 최소점에 수렴하는 방법을 찾는 것이라고 생각해도 좋을 것이다.
사실 위의 경사하강법 개선도 학습 성능 개선 방법 중 하나이다. 기본적으로 쓰여서 그렇지...
1. 아이리스 분류 풀 데이터셋 다시 살펴보기
10. 단층 퍼셉트론 을 다시 살펴보고 오자. 150개 오리지널 데이터셋을 한번 섞고(shuffle) 마지막 20개를 Test dataset으로 만들고 학습 모델을 평가하였다. 단순 argmax를 이용하였을 때 정확도 85%였지만 모델 예측 0.7 이상은 1, 그 외에는 0으로 엄밀하게 하였을 때 정확도 25%라는 기가막힌(...) 수치를 달성하였다.
22. 다중회귀-소프트맥스 함수 역전파(고급) 을 보고 오면 알겠지만 이 포스트에서 사용한 소프트맥스 역전파가 훨씬 더 안정적이여서 학습이 더 잘된다(...) 그래도 조금의 차이를 보이니 계속 작성해 나가보도록 하겠다.
2. 학습 내용 요약
예를 들어 데이터셋이 N개로 구성되어 있다면
1) Gradient Descent : 전체 데이터셋 N개를 한번에 학습(GD)
2) Stochastic Gradient Descent : N개 중 임의의 1개만을 선택하여 학습(SGD)
3) Mini batch Gradient Descent : 1 < Mini batch < N 개의 Mini batch 단위로 학습(Mini batch GD)
3-1) Mini batch Gradient Descent & Shuffle : 3)의 학습에서 batch를 만들기 전 전체 데이터를 셔플함.(Mini batch GD)
#주의할 점!
인터넷 상에서 batch와 Mini batch를 혼용하여 사용한다. batch는 전체 데이터셋을 말하고 Mini batch는 전체 데이터셋을 나눈 것을 의미한다. 그리고 3-1) 방법으로 학습하는 것을 SGD라고 이야기하는 경우도 많은데, 엄밀히 말하면 틀린 말이기는 하다.
하지만 최근들어 Mini batch를 batch로, 그리고 Mini batch GD & Shuffle 을 SGD로 혼용해서 언급하긴 한다. 잘 인지하길 바란다.
1) Gradient Descent
기본적인 방법으로 전체 데이터셋 N개를 한번에 학습하는 방법이다. 학습이 오래 걸리고 지역 최소점에 수렴하는 문제가 발생할 수 있다.
(1) 핵심 코드
# 학습 데이터의 정의
data = genfromtxt('IRIS_onehot.csv', delimiter=',', skip_header=1)
np.random.shuffle(data)
inputs = data[:130, 0:4]
targets = data[:130, 4:7]
test_inputs = data[130:, 0:4]
test_targets = data[130:, 4:7]
# 학습하기, 전체 Train dataset인 inputs와 targets를 한번에 학습한다.
for i in range(500):
G1, S, target_Y, pred, loss = forward(inputs, targets, W, B)
dL_dW, dL_dB = backward(G1, S, target_Y, inputs, targets)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
(2) 결과 : 학습률 0.001일 때 단순 최대 확률을 선택할 때 95%, 0.7 이상을 최대 확률로 선택할 때 90%
(3)오차값 변화 : 0 ~ 200 Epochs 사이에 선이 두껍게 되어 있는데 수렴값 주변에서 진동한 것이다.

(4) 전체코드
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
np.random.seed(220106)
data = genfromtxt('IRIS_onehot.csv', delimiter=',', skip_header=1)
np.random.shuffle(data)
inputs = data[:130, 0:4]
targets = data[:130, 4:7]
test_inputs = data[130:, 0:4]
test_targets = data[130:, 4:7]
W = np.random.randn(3, 4)
B = np.random.randn(3, 1)
learning_rate = 0.001 # 0.8
def forward(input, target, W, B):
X = np.transpose(input, (1, 0)) # (4, batch)
G = np.dot(W, X) + B # (3, batch)
exp = np.exp(G) # (3, batch)
sum_exp = np.sum(exp, axis=0, keepdims=True) #(1, batch)
S = exp/sum_exp # (3, batch)
pred = np.transpose(S, (1, 0)) # (batch, 3)
target_Y = np.sum(pred * target, axis=1, keepdims=True) # (batch, 1)
losses = np.sum(-np.log(target_Y)) # (1, 1)
return G, S, target_Y, pred, losses
def backward(G, S, target_Y, input, target):
dL_dS = -1/(np.transpose(target_Y, (1, 0))) # (1, batch)
# create softmax derivate matrix
grads = []
for s in np.transpose(S, (1, 0)):
grad_matrix = np.zeros((s.size, s.size))
for i in range(len(S)):
for j in range(len(s)):
if i == j:
grad_matrix[i][i] = s[i]*(1-s[i])
else:
grad_matrix[i][j] = - s[i]*s[j]
grads.append(grad_matrix.tolist()) # (batch, 3, 3)
# calculate dS/dG
grads = np.array(grads)
Y_target = np.expand_dims(target, axis=1) # (batch, 1, 3)
dS_dG = []
for i in range(len(Y_target)):
value = np.dot(grads[i], np.transpose(Y_target[i], (1, 0))) # (3, 1)
value = np.transpose(value, (1, 0)) # (1, 3)
dS_dG.append(value.tolist()) # (batch, 1, 3)
dS_dG = np.array(dS_dG) # (batch, 1, 3)
dS_dG = dS_dG.reshape(len(Y_target), -1) # (batch, 3)
dS_dG = np.transpose(dS_dG, (1, 0)) # (3, batch)
dG_dW = input # (batch, 4)
dG_dB = np.ones_like(G) # (3, batch)
# ∂L/∂W
dL_dG = dL_dS * dS_dG # (3, batch)
dL_dW = np.dot(dL_dG, dG_dW) # (3, 4)
dL_dB = np.sum(dL_dG * dG_dB, axis=1, keepdims=True) # (3, 1)
return dL_dW, dL_dB
_, _, _, pred, losses = forward(inputs, targets, W, B)
#print('before pred', pred)
print('before loss', losses)
arr_loss = []
for i in range(500):
G1, S, target_Y, pred, loss = forward(inputs, targets, W, B)
dL_dW, dL_dB = backward(G1, S, target_Y, inputs, targets)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
arr_loss.append(loss)
_, _, _, pred, losses = forward(inputs, targets, W, B)
#print('before pred', pred)
print('before loss', losses)
_, _, _, test_pred, losses = forward(test_inputs, test_targets, W, B)
equal_num = np.argmax(test_pred, axis=1) == np.argmax(test_targets, axis=1)
print('equal_num', equal_num)
print('accuracy', np.sum(equal_num/len(equal_num)))
"""
equal_num [False True True True True True True True True True True True
True True True True True True True True]
accuracy 0.9500000000000002
"""
filter_test_pred = np.where(test_pred >= 0.7, 1, 0)
filter_test_targets = np.array(test_targets, dtype=np.int16)
filter_equal_num = np.argmax(filter_test_pred, axis=1) == np.argmax(filter_test_targets, axis=1)
print('filter equal_num', filter_equal_num)
print('filter accuracy', np.sum(filter_equal_num/len(filter_equal_num)))
"""
filter equal_num [False True True True True True True True True True True True
True True True True True True False True]
filter accuracy 0.9000000000000001
"""
plt.plot(arr_loss)
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.show()2) Stochastic Gradient Descent
전체 데이터셋 중 임의의 1개만을 매번 선택하여 학습하는 방법이다. 학습이 빠르게 일어날 수 있으나 전체 최소점을 잘 못찾고 헤멜 가능성이 높다. 진동이 크다.
(1) 핵심 코드
for i in range(500):
SGD_num = np.random.randint(130) # 임의의 수를 선택하기 위한 정수 난수 생성
x = inputs[SGD_num].reshape(1, -1) # 2차원 배열로 만들기
y = targets[SGD_num].reshape(1, -1) # # 2차원 배열로 만들기
G1, S, target_Y, pred, loss = forward(x, y, W, B)
dL_dW, dL_dB = backward(G1, S, target_Y, x, y)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
(2) 결과 : 학습률 0.02일 때 단순 최대 확률을 선택할 때 65%, 0.7 이상을 최대 확률로 선택할 때 65%로 높지 않다. 계속 진동하기 때문이다. (학습률을 기존처럼 0.001을 하면 수렴하지 못하고 진동한다.)
(3)오차값 변화 : SGD 특성상 계속 진동하면서 수렴한다.

(4) 전체코드
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
np.random.seed(220106)
data = genfromtxt('IRIS_onehot.csv', delimiter=',', skip_header=1)
np.random.shuffle(data)
inputs = data[:130, 0:4]
targets = data[:130, 4:7]
test_inputs = data[130:, 0:4]
test_targets = data[130:, 4:7]
W = np.random.randn(3, 4)
B = np.random.randn(3, 1)
learning_rate = 0.02 # 0.8
def forward(input, target, W, B):
X = np.transpose(input, (1, 0)) # (4, batch)
G = np.dot(W, X) + B # (3, batch)
exp = np.exp(G) # (3, batch)
sum_exp = np.sum(exp, axis=0, keepdims=True) #(1, batch)
S = exp/sum_exp # (3, batch)
pred = np.transpose(S, (1, 0)) # (batch, 3)
target_Y = np.sum(pred * target, axis=1, keepdims=True) # (batch, 1)
losses = np.sum(-np.log(target_Y)) # (1, 1)
return G, S, target_Y, pred, losses
def backward(G, S, target_Y, input, target):
dL_dS = -1/(np.transpose(target_Y, (1, 0))) # (1, batch)
# create softmax derivate matrix
grads = []
for s in np.transpose(S, (1, 0)):
grad_matrix = np.zeros((s.size, s.size))
for i in range(len(S)):
for j in range(len(s)):
if i == j:
grad_matrix[i][i] = s[i]*(1-s[i])
else:
grad_matrix[i][j] = - s[i]*s[j]
grads.append(grad_matrix.tolist()) # (batch, 3, 3)
# calculate dS/dG
grads = np.array(grads)
Y_target = np.expand_dims(target, axis=1) # (batch, 1, 3)
dS_dG = []
for i in range(len(Y_target)):
value = np.dot(grads[i], np.transpose(Y_target[i], (1, 0))) # (3, 1)
value = np.transpose(value, (1, 0)) # (1, 3)
dS_dG.append(value.tolist()) # (batch, 1, 3)
dS_dG = np.array(dS_dG) # (batch, 1, 3)
dS_dG = dS_dG.reshape(len(Y_target), -1) # (batch, 3)
dS_dG = np.transpose(dS_dG, (1, 0)) # (3, batch)
dG_dW = input # (batch, 4)
dG_dB = np.ones_like(G) # (3, batch)
# ∂L/∂W
dL_dG = dL_dS * dS_dG # (3, batch)
dL_dW = np.dot(dL_dG, dG_dW) # (3, 4)
dL_dB = np.sum(dL_dG * dG_dB, axis=1, keepdims=True) # (3, 1)
return dL_dW, dL_dB
_, _, _, pred, losses = forward(inputs, targets, W, B)
#print('before pred', pred)
print('before loss', losses)
arr_loss = []
for i in range(500):
SGD_num = np.random.randint(130)
x = inputs[SGD_num].reshape(1, -1)
y = targets[SGD_num].reshape(1, -1)
G1, S, target_Y, pred, loss = forward(x, y, W, B)
dL_dW, dL_dB = backward(G1, S, target_Y, x, y)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
arr_loss.append(loss)
_, _, _, pred, losses = forward(inputs, targets, W, B)
#print('before pred', pred)
print('before loss', losses)
_, _, _, test_pred, losses = forward(test_inputs, test_targets, W, B)
equal_num = np.argmax(test_pred, axis=1) == np.argmax(test_targets, axis=1)
print('equal_num', equal_num)
print('accuracy', np.sum(equal_num/len(equal_num)))
"""
equal_num [False True True True True True True True True False False True
True True False True False True False False]
accuracy 0.6500000000000001
"""
filter_test_pred = np.where(test_pred >= 0.7, 1, 0)
filter_test_targets = np.array(test_targets, dtype=np.int16)
filter_equal_num = np.argmax(filter_test_pred, axis=1) == np.argmax(filter_test_targets, axis=1)
print('filter equal_num', filter_equal_num)
print('filter accuracy', np.sum(filter_equal_num/len(filter_equal_num)))
"""
filter equal_num [False True True True True True True True True False False True
True True False True False True False False]
filter accuracy 0.6500000000000001
"""
plt.plot(arr_loss)
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.show()3) Mini batch Gradient Descent
1 < Mini batch < N 개의 Mini batch 단위로 학습하는 방법이다. 전체 데이터를 한번에 학습하지 않고 Mini batch 단위로 나누어 학습한다. GD와 SGD의 절충 첫 단계이다.
(1) 핵심 코드
batch_size = 64
steps=0
def make_batch(input, target, step, batch_size):
if len(input) >= step + batch_size:
input_batch = input[step : step + batch_size]
target_batch = target[step : step + batch_size]
else:
input_batch = input[step : ]
target_batch = target[step : ]
return input_batch, target_batchMini batch로 나눌 단위인 batch_size를 설정한다. 2의 배수로 하는것이 좋다고 한다. 학습해 보면서 최적의 batch_size를 찾아보는 것이 좋다. make_batch 함수를 통해 64개의 행으로 자르고 리턴한다. 만약 남은 행이 batch_size보다 작다면 그 나머지를 리턴한다.
아래 코드를 참고하면 배치가 어떻게 분리되고 리턴되는지 알 수 있다.
import numpy as np
data = np.array([[1., 2., 0],
[3., 4., 0],
[5., 6., 0],
[7., 8., 0],
[9., 10., 1],
[11., 12., 1],
[13., 14., 1]])
#np.random.shuffle(data)
input = data[:, 0:2]
target = data[:, -1:]
def make_batch(X, Y, step, batch_size):
print('step', step)
if len(X) > step + batch_size:
X_batch = X[step : step + batch_size]
Y_batch = Y[step : step + batch_size]
else:
X_batch = X[step : ]
Y_batch = Y[step : ]
return X_batch, Y_batch
batch_size = 4
steps = 0
for i in range(10):
if steps > len(input):
steps = 0
np.random.shuffle(data)
x_batch, y_batch = make_batch(input, target, steps, batch_size)
print('x_batch', x_batch)
print('y_batch', y_batch)
steps = steps + batch_size
"""
step 0
x_batch [[1. 2.]
[3. 4.]
[5. 6.]
[7. 8.]]
y_batch [[0.]
[0.]
[0.]
[0.]]
step 4
x_batch [[ 9. 10.]
[11. 12.]
[13. 14.]]
y_batch [[1.]
[1.]
[1.]]
step 0
x_batch [[ 3. 4.]
[ 5. 6.]
[ 7. 8.]
[11. 12.]]
y_batch [[0.]
[0.]
[0.]
[1.]]
step 4
x_batch [[ 9. 10.]
[ 1. 2.]
[13. 14.]]
y_batch [[1.]
[0.]
[1.]]
step 0
x_batch [[ 7. 8.]
[ 5. 6.]
[11. 12.]
[13. 14.]]
y_batch [[0.]
[0.]
[1.]
[1.]]
step 4
x_batch [[ 3. 4.]
[ 9. 10.]
[ 1. 2.]]
y_batch [[0.]
[1.]
[0.]]
step 0
x_batch [[7. 8.]
[5. 6.]
[3. 4.]
[1. 2.]]
y_batch [[0.]
[0.]
[0.]
[0.]]
step 4
x_batch [[ 9. 10.]
[13. 14.]
[11. 12.]]
y_batch [[1.]
[1.]
[1.]]
step 0
x_batch [[11. 12.]
[ 1. 2.]
[ 5. 6.]
[13. 14.]]
y_batch [[1.]
[0.]
[0.]
[1.]]
step 4
x_batch [[ 3. 4.]
[ 9. 10.]
[ 7. 8.]]
y_batch [[0.]
[1.]
[0.]]
"""
학습 시 mini batch 단위로 학습한다. steps를 0으로 설정하고 마지막 배치가 리턴될 때마다 초기화 시켜 첫 부분부터 배치를 리턴하게 한다.
for i in range(500):
if steps > len(inputs):
steps = 0
x_batch, y_batch = make_batch(inputs, targets, steps, batch_size)
G1, S, target_Y, pred, loss = forward(x_batch, y_batch, W, B)
dL_dW, dL_dB = backward(G1, S, target_Y, x_batch, y_batch)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
steps += batch_size
(2) 결과 : 학습률 0.001일 때 단순 최대 확률을 선택할 때 100%, 0.7 이상을 최대 확률로 선택할 때 85% 이다.
(3)오차값 변화 : 진동하지 않고 깔끔하게 수렴한다.
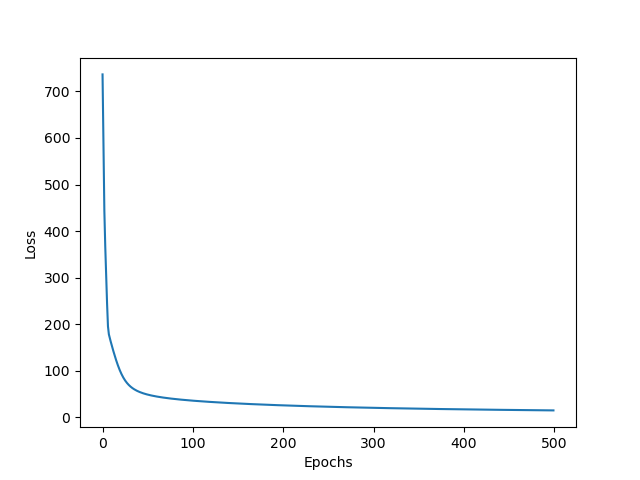
(4) 전체코드
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
np.random.seed(220106)
data = genfromtxt('IRIS_onehot.csv', delimiter=',', skip_header=1)
np.random.shuffle(data)
inputs = data[:130, 0:4]
targets = data[:130, 4:7]
test_inputs = data[130:, 0:4]
test_targets = data[130:, 4:7]
W = np.random.randn(3, 4)
B = np.random.randn(3, 1)
learning_rate = 0.001 # 0.8
batch_size = 64
steps=0
def make_batch(input, target, step, batch_size):
if len(input) >= step + batch_size:
input_batch = input[step : step + batch_size]
target_batch = target[step : step + batch_size]
else:
input_batch = input[step : ]
target_batch = target[step : ]
return input_batch, target_batch
def forward(input, target, W, B):
X = np.transpose(input, (1, 0)) # (4, batch)
G = np.dot(W, X) + B # (3, batch)
exp = np.exp(G) # (3, batch)
sum_exp = np.sum(exp, axis=0, keepdims=True) #(1, batch)
S = exp/sum_exp # (3, batch)
pred = np.transpose(S, (1, 0)) # (batch, 3)
target_Y = np.sum(pred * target, axis=1, keepdims=True) # (batch, 1)
losses = np.sum(-np.log(target_Y)) # (1, 1)
return G, S, target_Y, pred, losses
def backward(G, S, target_Y, input, target):
dL_dS = -1/(np.transpose(target_Y, (1, 0))) # (1, batch)
# create softmax derivate matrix
grads = []
for s in np.transpose(S, (1, 0)):
grad_matrix = np.zeros((s.size, s.size))
for i in range(len(S)):
for j in range(len(s)):
if i == j:
grad_matrix[i][i] = s[i]*(1-s[i])
else:
grad_matrix[i][j] = - s[i]*s[j]
grads.append(grad_matrix.tolist()) # (batch, 3, 3)
# calculate dS/dG
grads = np.array(grads)
Y_target = np.expand_dims(target, axis=1) # (batch, 1, 3)
dS_dG = []
for i in range(len(Y_target)):
value = np.dot(grads[i], np.transpose(Y_target[i], (1, 0))) # (3, 1)
value = np.transpose(value, (1, 0)) # (1, 3)
dS_dG.append(value.tolist()) # (batch, 1, 3)
dS_dG = np.array(dS_dG) # (batch, 1, 3)
dS_dG = dS_dG.reshape(len(Y_target), -1) # (batch, 3)
dS_dG = np.transpose(dS_dG, (1, 0)) # (3, batch)
dG_dW = input # (batch, 4)
dG_dB = np.ones_like(G) # (3, batch)
# ∂L/∂W
dL_dG = dL_dS * dS_dG # (3, batch)
dL_dW = np.dot(dL_dG, dG_dW) # (3, 4)
dL_dB = np.sum(dL_dG * dG_dB, axis=1, keepdims=True) # (3, 1)
return dL_dW, dL_dB
_, _, _, pred, losses = forward(inputs, targets, W, B)
#print('before pred', pred)
print('before loss', losses)
arr_loss = []
for i in range(500):
if steps > len(inputs):
steps = 0
x_batch, y_batch = make_batch(inputs, targets, steps, batch_size)
G1, S, target_Y, pred, loss = forward(x_batch, y_batch, W, B)
dL_dW, dL_dB = backward(G1, S, target_Y, x_batch, y_batch)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
steps += batch_size
arr_loss.append(loss)
_, _, _, pred, losses = forward(inputs, targets, W, B)
#print('before pred', pred)
print('before loss', losses)
_, _, _, test_pred, losses = forward(test_inputs, test_targets, W, B)
equal_num = np.argmax(test_pred, axis=1) == np.argmax(test_targets, axis=1)
print('equal_num', equal_num)
print('accuracy', np.sum(equal_num/len(equal_num)))
"""
equal_num [ True True True True True True True True True True True True
True True True True True True True True]
accuracy 1.0000000000000002
"""
filter_test_pred = np.where(test_pred >= 0.7, 1, 0)
filter_test_targets = np.array(test_targets, dtype=np.int16)
filter_equal_num = np.argmax(filter_test_pred, axis=1) == np.argmax(filter_test_targets, axis=1)
print('filter equal_num', filter_equal_num)
print('filter accuracy', np.sum(filter_equal_num/len(filter_equal_num)))
"""
filter equal_num [False True True True True True True True True True True False
True True True True True True False True]
filter accuracy 0.8500000000000002
"""
plt.plot(arr_loss)
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.show()3-1) Mini batch Gradient Descent & Shuffle
3)의 학습에서 배치 단위 학습이 끝나고 새로운 batch를 만들기 전, 전체 데이터를 셔플한다. GD와 SGD의 절충이다.
(1) 핵심 코드
data = genfromtxt('IRIS_onehot.csv', delimiter=',', skip_header=1)
np.random.shuffle(data)
train_data = data[:130, :]
test_data = data[130:, :]
inputs = train_data[:, 0:4]
targets = train_data[:, 4:7]
test_inputs = test_data[:, 0:4]
test_targets = test_data[:, 4:7]조금 더 복잡하게 나누어야 하는데 먼저 train 데이터와 test 데이터를 따로 나눈다. 왜냐하면 test 데이터는 분리전에만 셔플하고 앞으로 shuffle 하지 않을 것이기 때문이다.
for i in range(2000):
if steps > len(inputs):
steps = 0
np.random.shuffle(train_data)
x_batch, y_batch = make_batch(inputs, targets, steps, batch_size)
G1, S, target_Y, pred, loss = forward(x_batch, y_batch, W, B)
dL_dW, dL_dB = backward(G1, S, target_Y, x_batch, y_batch)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
steps += batch_sizesteps=0으로 초기화 될 때 새로운 배치를 만드는 데 만들기 전에 train data를 셔플해 준다.
(2) 결과 : 학습률 0.001일 때 단순 최대 확률을 선택할 때 95%, 0.7 이상을 최대 확률로 선택할 때 90% 이다.
(3)오차값 변화 : 3)인 Mini batch GD 보다 빠르게 수렴한다.
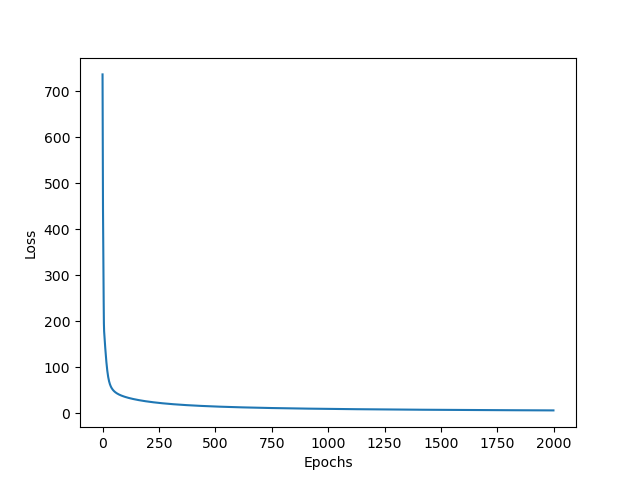
직접 비교해 보자. 빨간 색 원 안을 주목하길 바란다. 그래프가 x 축에 더 가까울 수록 빨리 수렴한다는 뜻이다.
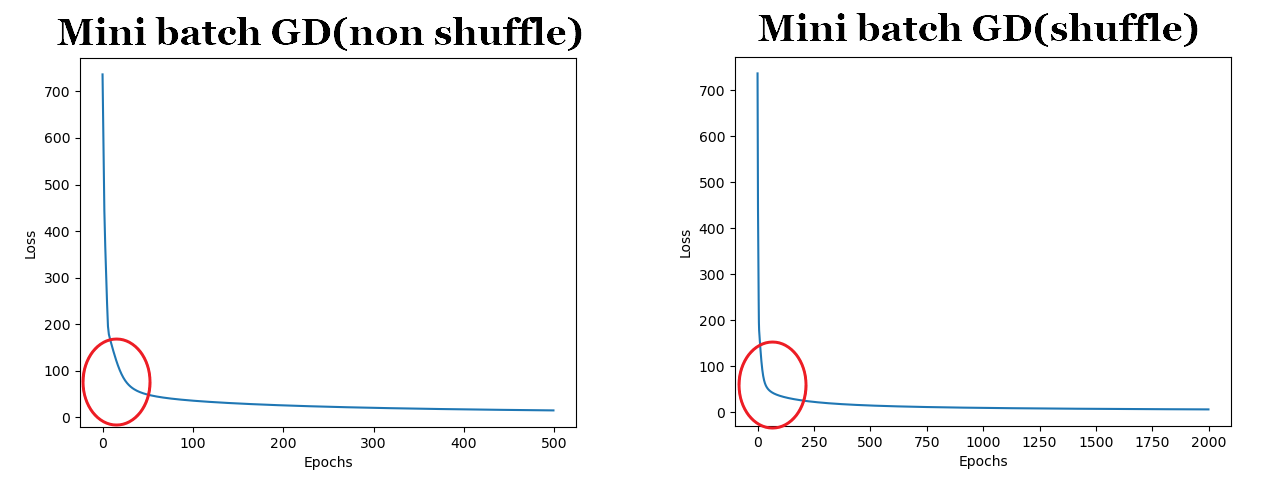
(4) 전체코드
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
np.random.seed(220106)
data = genfromtxt('IRIS_onehot.csv', delimiter=',', skip_header=1)
np.random.shuffle(data)
train_data = data[:130, :]
test_data = data[130:, :]
inputs = train_data[:, 0:4]
targets = train_data[:, 4:7]
test_inputs = test_data[:, 0:4]
test_targets = test_data[:, 4:7]
W = np.random.randn(3, 4)
B = np.random.randn(3, 1)
learning_rate = 0.001 # 0.8
batch_size = 64
steps=0
def make_batch(input, target, step, batch_size):
if len(input) >= step + batch_size:
input_batch = input[step : step + batch_size]
target_batch = target[step : step + batch_size]
else:
input_batch = input[step : ]
target_batch = target[step : ]
return input_batch, target_batch
def forward(input, target, W, B):
X = np.transpose(input, (1, 0)) # (4, batch)
G = np.dot(W, X) + B # (3, batch)
exp = np.exp(G) # (3, batch)
sum_exp = np.sum(exp, axis=0, keepdims=True) #(1, batch)
S = exp/sum_exp # (3, batch)
pred = np.transpose(S, (1, 0)) # (batch, 3)
target_Y = np.sum(pred * target, axis=1, keepdims=True) # (batch, 1)
losses = np.sum(-np.log(target_Y)) # (1, 1)
return G, S, target_Y, pred, losses
def backward(G, S, target_Y, input, target):
dL_dS = -1/(np.transpose(target_Y, (1, 0))) # (1, batch)
# create softmax derivate matrix
grads = []
for s in np.transpose(S, (1, 0)):
grad_matrix = np.zeros((s.size, s.size))
for i in range(len(S)):
for j in range(len(s)):
if i == j:
grad_matrix[i][i] = s[i]*(1-s[i])
else:
grad_matrix[i][j] = - s[i]*s[j]
grads.append(grad_matrix.tolist()) # (batch, 3, 3)
# calculate dS/dG
grads = np.array(grads)
Y_target = np.expand_dims(target, axis=1) # (batch, 1, 3)
dS_dG = []
for i in range(len(Y_target)):
value = np.dot(grads[i], np.transpose(Y_target[i], (1, 0))) # (3, 1)
value = np.transpose(value, (1, 0)) # (1, 3)
dS_dG.append(value.tolist()) # (batch, 1, 3)
dS_dG = np.array(dS_dG) # (batch, 1, 3)
dS_dG = dS_dG.reshape(len(Y_target), -1) # (batch, 3)
dS_dG = np.transpose(dS_dG, (1, 0)) # (3, batch)
dG_dW = input # (batch, 4)
dG_dB = np.ones_like(G) # (3, batch)
# ∂L/∂W
dL_dG = dL_dS * dS_dG # (3, batch)
dL_dW = np.dot(dL_dG, dG_dW) # (3, 4)
dL_dB = np.sum(dL_dG * dG_dB, axis=1, keepdims=True) # (3, 1)
return dL_dW, dL_dB
_, _, _, pred, losses = forward(inputs, targets, W, B)
#print('before pred', pred)
print('before loss', losses)
arr_loss = []
for i in range(2000):
if steps > len(inputs):
steps = 0
np.random.shuffle(train_data)
x_batch, y_batch = make_batch(inputs, targets, steps, batch_size)
G1, S, target_Y, pred, loss = forward(x_batch, y_batch, W, B)
dL_dW, dL_dB = backward(G1, S, target_Y, x_batch, y_batch)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
steps += batch_size
arr_loss.append(loss)
_, _, _, pred, losses = forward(inputs, targets, W, B)
#print('before pred', pred)
print('before loss', losses)
_, _, _, test_pred, losses = forward(test_inputs, test_targets, W, B)
equal_num = np.argmax(test_pred, axis=1) == np.argmax(test_targets, axis=1)
print('equal_num', equal_num)
print('accuracy', np.sum(equal_num/len(equal_num)))
"""
equal_num [False True True True True True True True True True True True
True True True True True True True True]
accuracy 0.9500000000000002
"""
filter_test_pred = np.where(test_pred >= 0.7, 1, 0)
filter_test_targets = np.array(test_targets, dtype=np.int16)
filter_equal_num = np.argmax(filter_test_pred, axis=1) == np.argmax(filter_test_targets, axis=1)
print('filter equal_num', filter_equal_num)
print('filter accuracy', np.sum(filter_equal_num/len(filter_equal_num)))
"""
filter equal_num [False True True True True True True True True True True True
True True True True True True False True]
filter accuracy 0.9000000000000001
"""
plt.plot(arr_loss)
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.show()
딥러닝엔 정답이 없다고 하지만 일반적으로 3)-1 처럼 데이터를 셔플하고 mini batch 단위로 학습하면 빠르게 전역 최소점으로 수렴하는 것으로 알려져 있다.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 25 - Deep Neural Nets 구현하기 (0) | 2022.04.20 |
|---|---|
| 24. 딥러닝에서 데이터 표준화, 정규화가 필요한 이유 (0) | 2022.04.19 |
| 22. 다중회귀-소프트맥스 함수 역전파(고급, 쉬운 방법) (0) | 2022.02.10 |
| 21. 경사하강법의 개선 - Adam (0) | 2022.02.05 |
| 20. 경사하강법의 개선 - Momentum, RMSprop (0) | 2022.02.04 |



