지금까지 했던 모델들은 모두 단층 퍼셉트론(또는 싱글 퍼셉트론) 연산이다.
Numpy 딥러닝 시리즈를 보면 모두 단층 퍼셉트론으로 어설픈(?) 딥러닝을 구현한 것을 알 수 있을 것이다.
구체적으로 어떤 것을 했었는지 살펴보자.
1. 복습
1) '1.선형회귀 구현하기'
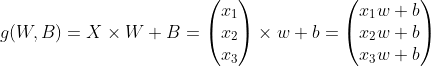
2) '3.입력 특성이 2개인 선형회귀 구현'

3) '4. 로지스틱 회귀 구현하기'
평균 득점(avg_score), 리바운드 횟수(rebound), 어시스트 횟수(asist)에 따른 신인 농구 선수의 NBA 드래프트 여부 (1:성공, 0:실패) 구현하기
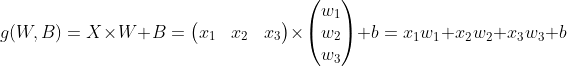
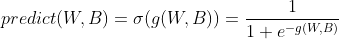
4) '7. 다중 분류 구현하기'
Iris 꽃 4개의 특성을 입력 받아 3개의 꽃으로 분류하기
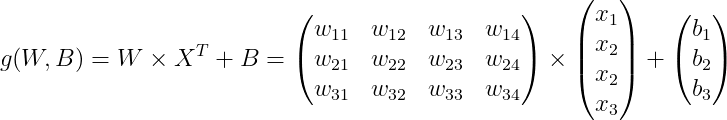

2. 퍼셉트론
퍼셉트론(Perceptron)은 1943년에 제안된 아이디어로 쉽게 설명하자면 위의 예시처럼
입력(Input) * 가중치(Weight + Bias) + 의 연산을 활성화함수에 통과시킨 출력값을 목표값과 비교하고 가중치를 업데이트하여 학습하는 것을 의미한다. 이전부터 우리가 계속 해 왔던 것이다.

활성화 함수는 선형 연산(input * weight)의 요소들의 합을 출력신호로 변환하는 것이다.
로지스틱 회귀 예시에서
입력 신호는 평균 득점(avg_score), 리바운드 횟수(rebound), 어시스트 횟수(asist) 3가지였다.
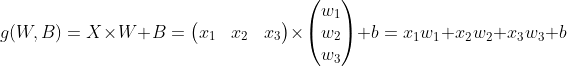
드래프트 여부는 0(드래프트 실패) 1(드래프트 성공) 으로 판별되는데 위 값 자체로는 0과 1로 연결되지 않는다. 활성화 함수는 연산 결과를 0과 1로 변환해주는 역할을 한다. Iris 꽃 분류도 4개의 데이터를 입력 받아 연산을 하고 3개의 확률로 변환하기 위해 소프트맥스 활성화함수를 사용하였다.
3. 아이리스 분류 풀 데이터셋으로 다시 풀어보기
아이리스 분류 150개의 풀 데이터셋이다. (tiny 버전은 학습과정과 결과를 눈에 볼 수 있도록 만든 버전이다.) 오리지널 데이터셋으로 kaggle에서 받을 수 있다.
1) 데이터 전처리
데이터 세트를 보면 알겠지만 classes가 순서대로 되어 있기 때문에 전혀 훈련이 되지 않아 데이터세트를 분할하기 전에 섞어준다. 단층 퍼셉트론의 성능을 확인하기 위해 150개의 데이터세트 중 130개를 훈련 세트(train data), 나머지 20개를 테스트 세트(test data)로 지정할 것이다. 또한 이대로 실행하면 exp에서 overflow가 발생하므로 입력 데이터에 0.1을 곱해준다.
위 설명을 코드로 작성하면 아래와 같다.
data = genfromtxt('IRIS_onehot.csv', delimiter=',', skip_header=1)
np.random.shuffle(data)
input = data[:130, 0:4]*0.1
target = data[:130, 4:7]
test_input = data[130:, 0:4]*0.1
test_target = data[130:, 4:7]
그 외의 코드는 이전 포스트와 동일하다.
2) 결과 평가하기
훈련되지 않은 나머지 20개의 test data 세트로 평가를 해 보자.
첫 번째 방법으로, 가장 큰 확률을 1, 그 외에는 0으로 두는 것이다. 이를 확인하기 위해 argmax를 사용한다.
np.argmax는 배열 요소 중 최대값의 인덱스를 반환한다.
즉 np.argmax(test_pred, axis=1)은 [0.6, 0.3, 0.1]로 예측된 모델에서는 0을, [0.1, 0.2, 0.7]에서는 2을 반환한다.
np.argmax(test_target, axis=1)도 마찬가지이다. [0, 1, 0] 이라면 1을 반환한다.
equal_num은 np.argmax(test_pred, axis=1) 배열과 np.argmax(test_target, axis=1) 배열의 요소가 일치하면 True, 일치하지 않으면 False를 반환한다.
예를 들어 [1, 2, 3, 4] == [0, 2, 5, 7] 이라면 [False, True, False, False] 이다.
accuracy(정확도)는 (True 갯수 / 배열 요소 개수) 로 구할 수있다.
test_pred, _ = softmax_forward(test_input, test_target, W, B)
equal_num = np.argmax(test_pred, axis=1) == np.argmax(test_target, axis=1)
print('equal_num', equal_num)
print('accuracy', np.sum(equal_num/len(equal_num)))
이렇게 실시했을 때의 결과는 아래와 같다.
equal_num [ True True True True True True True True True True True True
True True False True False True True False]
accuracy 0.8500000000000001
정답률이 85%라고? 잘된 것 아닌가? 싶지만 짚어봐야 할 것이 있다. 제대로 된 훈련이라면 확률이 1에 가까워야 할 것이다. 저번 시간 포스트 결과를 보면 알겠지만 실제로 확률이 1에 가깝지 않다.
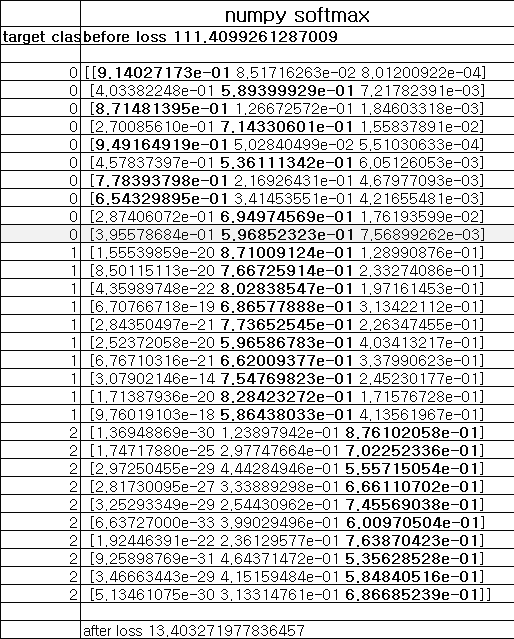
두 번째 방법은 좀 더 엄밀하게 할 것이다. test pred 값에서 가장 확률이 높은 값이 0.7 이상이면 1, 그 외에는 0으로 만든다. 첫 번째 방법은 0.5라도 가장 큰 값이면 1로 만들었는데 제대로 훈련 되었는지 확인하기 위해서 높은 확률이어야 한다는 전제를 둔 것이다. 이를 위해 numpy where를 이용한다. where(condition, a, b)는 condition이 참이면 a, 거짓이면 b를 실행한다. 그리고 위에서 처럼 argmax로 인덱스가 일치하는지 확인한다.
filter_test_pred = np.where(test_pred >= 0.7, 1., 0.)
filter_equal_num = np.argmax(filter_test_pred, axis=1) == np.argmax(test_target, axis=1)
print('filter equal_num', filter_equal_num)
print('filter accuracy', np.sum(filter_equal_num/len(filter_equal_num)))
결과는 아래와 같다.
filter equal_num [False True True False False True False False True False False False
False True False False False False False False]
filter accuracy 0.25
결과는 처참하다(...) 훈련은 되었지만 정확하고 깔끔하게 훈련되지 않았다는 뜻이다.
아래는 전체 코드이다.
import numpy as np
from numpy import genfromtxt
np.random.seed(220106)
data = genfromtxt('IRIS_onehot.csv', delimiter=',', skip_header=1)
np.random.shuffle(data)
input = data[:130, 0:4]*0.1
target = data[:130, 4:7]
test_input = data[130:, 0:4]*0.1
test_target = data[130:, 4:7]
W = np.random.randn(3, 4)
B = np.random.randn(3, 1)
# shuffle when trainning
#learning_rate = 0.001 # 0.75
#learning_rate = 0.0005 # 0.75
# not shuffle
learning_rate = 0.001 # 0.65
learning_rate = 0.0005 # 0.5
batch_size = 16
def softmax_forward(X, Y, W, B):
arr_pred = []
arr_loss = []
for i in range(len(X)):
x = [X[i]]
y = [Y[i]]
# preprocessing data for calculate
x = np.transpose(x )
WXB = np.dot(W, x) + B
e_WXB1 = np.exp(WXB[0])
e_WXB2 = np.exp(WXB[1])
e_WXB3 = np.exp(WXB[2])
sum_e_WXB = e_WXB1 + e_WXB2 + e_WXB3
smax_WXB1 = e_WXB1 / sum_e_WXB
smax_WXB2 = e_WXB2 / sum_e_WXB
smax_WXB3 = e_WXB3 / sum_e_WXB
softmax = np.array([smax_WXB1[0], smax_WXB2[0], smax_WXB3[0]])
arr_pred.append(softmax)
y_target = np.sum(softmax * y, axis = 1, keepdims=True)
loss = -np.log(y_target)
arr_loss.append(loss)
preds = np.array(arr_pred)
losses = np.sum(np.array(arr_loss))
return preds, losses
def loss_gradient(X, Y, W, B):
add_dL_dW = np.zeros((3, 4))
add_dL_dB = np.zeros((3, 1))
for i in range(len(X)):
x = [X[i]]
y = [Y[i]]
# preprocessing data for calculate
x = np.transpose(x )
WXB = np.dot(W, x) + B
e_WXB1 = np.exp(WXB[0])
e_WXB2 = np.exp(WXB[1])
e_WXB3 = np.exp(WXB[2])
sum_e_WXB = e_WXB1 + e_WXB2 + e_WXB3
smax_WXB1 = e_WXB1 / sum_e_WXB
smax_WXB2 = e_WXB2 / sum_e_WXB
smax_WXB3 = e_WXB3 / sum_e_WXB
softmax = np.array([smax_WXB1[0], smax_WXB2[0], smax_WXB3[0]])
y_target = np.sum(softmax * y, axis = 1, keepdims=True)
#∂L(smax(g(W, B))) / ∂smax(g(W,B))
dL_dsmax = -1 / y_target
#smax 도함수 행렬(3x3)
dsmax_dg_matrix = np.array([[(smax_WXB1*(1-smax_WXB1))[0], -(smax_WXB1*smax_WXB2)[0], -(smax_WXB1*smax_WXB3)[0]],
[-(smax_WXB1*smax_WXB2)[0], (smax_WXB2*(1-smax_WXB1))[0], -(smax_WXB2*smax_WXB3)[0]],
[-(smax_WXB1*smax_WXB3)[0], -(smax_WXB2*smax_WXB3)[0], (smax_WXB2*(1-smax_WXB1))[0]]])
#∂smax(g(W, B)) / ∂g(W,B) -> smax 도함수 행렬(3x3)에 target Y를 곱하여 해당 값 추출
dsmax_dg = np.dot(dsmax_dg_matrix, np.transpose(y, (1, 0)))
#∂g(W, B) / ∂W
dg_dW = np.transpose(x, (1, 0))
# ∂smax(g(W, B)) / ∂W = ∂smax(g(W, B)) / ∂g(W,B) * ∂g(W, B) / ∂W
dsmax_dW = np.dot(dsmax_dg, dg_dW)
# ∂L(g(W, B)) / ∂W = ∂L / ∂smax(g(W, B)) * ∂smax(g(W, B)) / ∂W
dL_dW = dL_dsmax* dsmax_dW
# ∂L(g(W, B)) / ∂W 더하여 누적
add_dL_dW = add_dL_dW + dL_dW
# ∂L(g(W, B)) / ∂B = ∂L / ∂smax(g(W, B)) * ∂smax(g(W, B)) / ∂g(W, B) * ∂g(W, B) / ∂B(-> 1임)
dL_dB = dL_dsmax * dsmax_dg
# ∂L(g(W, B)) / ∂B 더하여 누적
add_dL_dB = add_dL_dB + dL_dB
return add_dL_dW, add_dL_dB
pred, loss = softmax_forward(input, target, W, B)
#print('before pred', pred)
print('before loss', loss)
for i in range(2000):
dL_dW, dL_dB = loss_gradient(input, target, W , B)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
pred, loss = softmax_forward(input, target, W, B)
#print('after pred', pred)
print('after loss', loss)
test_pred, _ = softmax_forward(test_input, test_target, W, B)
equal_num = np.argmax(test_pred, axis=1) == np.argmax(test_target, axis=1)
print('equal_num', equal_num)
print('accuracy', np.sum(equal_num/len(equal_num)))
"""
equal_num [ True True True True True True True True True True True True
True True False True False True True False]
accuracy 0.8500000000000001
"""
filter_test_pred = np.where(test_pred >= 0.7, 1., 0.)
filter_equal_num = np.argmax(filter_test_pred, axis=1) == np.argmax(test_target, axis=1)
print('filter equal_num', filter_equal_num)
print('filter accuracy', np.sum(filter_equal_num/len(filter_equal_num)))
"""
filter equal_num [False True True False False True False False True False False False
False True False False False False False False]
filter accuracy 0.25
"""
4. 퍼셉트론의 한계
여러 가지 이유가 있는데 위 사례를 보자면 데이터가 복잡해 질 수록 단순한 선형 연산과 활성화함수 만으로 학습이 어렵다. 간단하고 경향성이 큰 데이터에서는 퍼셉트론 모델이 쓸만한데, 일상에서 겪는 복잡한 관계나 데이터셋으로는 한계가 있다는 것이다.
다음 시간에 단층 퍼셉트론의 한계 사례 2가지를 더 언급하고자 한다.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 12. 단층 퍼셉트론의 한계-2.선형 회귀식의 한계 (0) | 2022.01.12 |
|---|---|
| 11. 단층 퍼셉트론의 한계-1.XOR 문제 (0) | 2022.01.11 |
| 9. 다중 분류 구현하기(심화실습) (2) | 2022.01.09 |
| 8. 다중 분류 구현하기(기초실습) (0) | 2022.01.09 |
| 7. 다중 분류 구현하기(이론) (0) | 2022.01.08 |



