이번 시간에는 소프트맥스 함수로 출력되는 다중 분류 구현하기를 이론적으로 살펴보겠다. 대표적인 문제로 아이리스(Iris) 꽃 분류 문제가 있다. 아래 자료를 살펴보자.
1. 데이터 살펴보기

1) 데이터 속성 : 4가지
(1) sepal_length : 꽃잎 길이
(2) sepal_width : 꽃잎 너비
(3) petal_lenth : 꽃받침 길이
(4) petal_width : 꽃받침 너비
2) 데이터 분류 : 3가지(setosa, versicolor, virginica)

4가지의 데이터 속성을 입력받아 3가지의 아이리스 꽃 분류를 하는 문제이다.
2. 정의하기
1) 입력값(input)을 아래와 같이 정의한다.
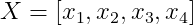
2) 목표값(target) 아래와 같이 정의한다.

3) 가중치(weight)와 편향(bias)를 정의한다.
입력은 (1, 4) 출력은 (3, 1) 이다. 따라서 weight(W)는 (3, 4), bias(B)는 (3, 1)이다.
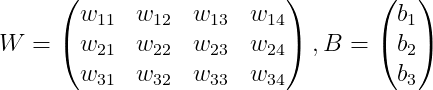
4) g(W, B) 연산은 아래와 같이 정의한다.
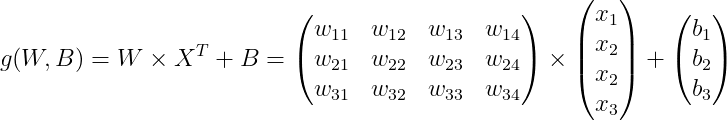

5) S(W, B) 연산은 아래와 같이 정의한다. -> 신경망의 출력이 된다.

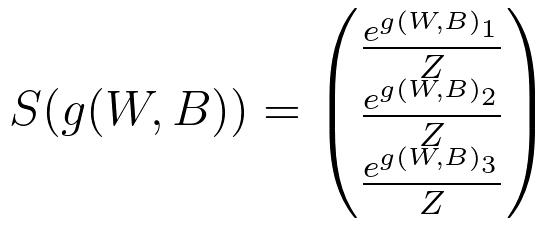
즉, g(WB)1 / Z은 setosa 일 확률, g(WB)2 / Z는 versicolor일 확률, g(WB)3 / Z는 virginica일 확률이다.
이것이 최종 출력이고 올바른 확률로 출력할 수 있도록 학습시키는 것이 목표이다.
6) 손실함수 정의하기
손실함수 L(W, B) 는 아래와 같이 정의된다. 크로스 엔트로피(Cross entropy)이다.

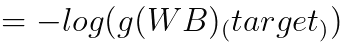
이게 왜 이렇게 되냐면 Y는 2)에서 볼 수 있다싶이 0과 1로 인코딩된 행렬인데
Y들의 요소(3, 1) 와 S(g(W, B))에 log를 씌운 값(3, 1)과 단순 곱을 하고 더하는 것이다. 이 과정에서 실제 정답만 1이고 나머지는 0 이므로 0이 곱해진 log값은 사라지고 정답인 log(g(WB)target) 값만 살아남기 때문이다.
예를 들면 결과가 (1, 0, 0), setosa가 정답인 경우 g(WB)1만 살아남는다.

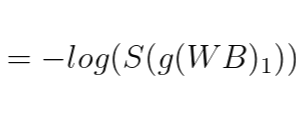
3. 손실함수의 도함수 정의하기(난이도 상승 주의)
이전과 마찬가지로 체인룰을 이용하여 W, B에 따른 손실함수의 도함수를 정의하겠다.
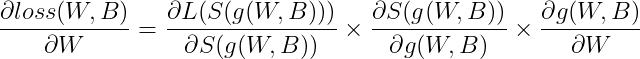

주의할점!!! 여기서 g(W,B)는 정답 요소 g(W,B)target 이다. 왜냐하면 최종 계산에서 target이 아닌 값들은 0에 곱해져 사라졌기 때문이다. (위의 6) 손실함수 정의하고 참고)
g(W,B)가 target인 경우는 3가지 임을 기억하자.
(1) g(W,B)1이 target일 때 -> Y는 (1, 0, 0)
(2) g(W,B)2이 target일 때 -> Y는 (0, 1, 0)
(3) g(W,B)3이 target일 때 -> Y는 (0, 0, 1)
1) ∂L(S(g(W,B))) / ∂S(g(W,B)) 유도하기
로그의 미분을 이용하여 구한다.

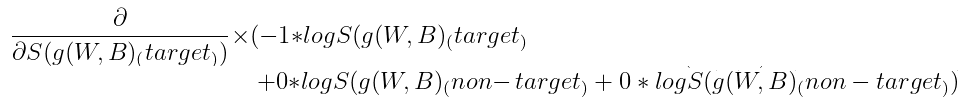

2) ∂S(g(W,B)) / ∂g(W,B) 유도하기
(1) 먼저 S(g(W,B)1)값을 σ(S(g(W,B)1) 표기로 정의한다. 이런식으로 σ(S(g(W,B)2), σ(S(g(W,B)3)도 정의할 수 있다.

(2) 아래는 소프트맥스 함수를 어떤 요소로 미분하느냐에 따라 달라지는 결과 예시를 보여준다.
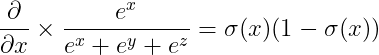

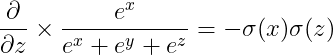
(3) ∂S(g(W,B)) / ∂g(W,B) 행렬은 아래와 같이 표기할 수 있다.

(4) 여기서 어떤 것이 target인가에 따라 달라진다. 왜냐하면 L(S(g(W,B))) 계산에서 target이 아닌 것은 0을 곱하여 제거하기 때문이다. target이 g(W,B)1, g(W,B)2, g(W,B)3 인 경우 ∂S(g(W,B)) / ∂g(W,B) 계산 결과 행렬은 각각 순서대로 아래와 같다.

(5) 3개인 경우로 분할해서 따로 놓는 것은 하나도 아름답지 않다. 수학은 모름지기 간결해야 한다. 타겟이 어떠한지 간에 한번에 계산할 수 있는 방법이 없을까? 아래처럼 미분행렬과 타겟행렬을 곱한다면 위의 미분행렬이 나온다. 따라서 이번 이론에서 유도할 최종 ∂S(g(W,B)) / ∂g(W,B) 미분식은 아래와 같다.

3) ∂g(W,B) / ∂W 유도하기
Numpy 딥러닝 구현하기 거의 처음에 이 부분을 증명하여서 생략한다. 답은 X의 전치행렬이다.
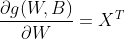
궁금하면 target이 각각 g(W,B)1, g(W,B)2, g(W,B)3일 때 아래의 식을 계산해 보자
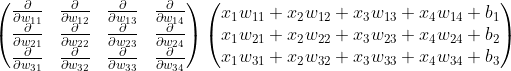
헷갈리는 점이 있는데 일반적으로 데이터구조를 만들 때 입력 데이터 X를 [x1, x2, x3, x4] 식으로(1, 4) shape의 열(column)을 데이터 특성(feature)로 지정하는데 이번 g(W,B) 계산에서 (3, 1) 로 출력하기 위해 X를 전치(transpose) 하여 (4, 1) shape으로 계산하였다. 따라서 다시 전치를 하게 되면 원래 입력 데이터 shape인 (1, 4)로 돌아온다. 그리고 X의 전치행렬을 맨 뒤에 곱한다는 것도 눈여겨 볼 점이다. 이 점만 주의하자.
4) ∂g(W,B) / ∂B 유도하기
마찬가지로 이전에 유도하였기 때문에 생략하겠다. 답은 (3, 1) shape의 값이 1인 행렬이다. 단순한 곱하기라 생략.
4. 도함수 정의하기
1) ∂loss(W,B) / ∂W 는 아래와 같이 정의된다.
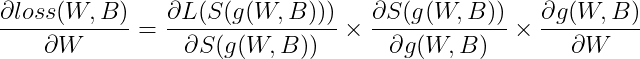
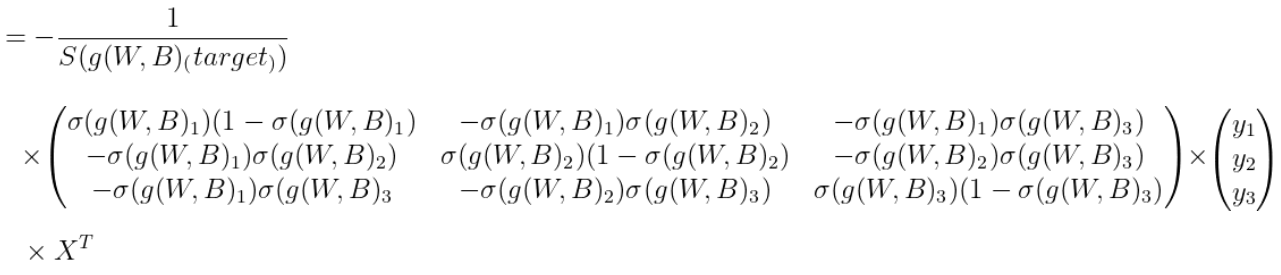
곱 순서대로 shape을 살펴보면 scalar X (3, 3) X (3, 1) X (1, 4) = (3, 4) 행렬이 나온다. W 행렬이 (3, 4) 이므로 올바르게 구한 것을 확인할 수 있다.
1) ∂loss(W,B) / ∂B 는 아래와 같이 정의된다.

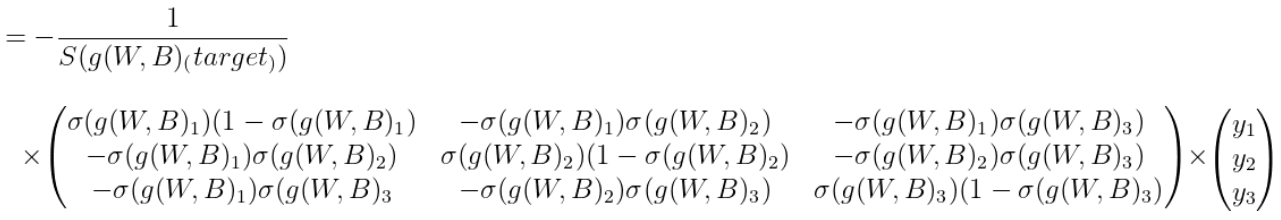
곱 순서대로 shape을 살펴보면 scalar X (3, 3) X (3, 1) = (3, 1) 행렬이 나온다. B 행렬이 (3, 1) 이므로 올바르게 구한 것을 확인할 수 있다.
정말 식이 길었다. 사실 앞으로 가야 할 길이 더욱 많다 ㅋㅋㅋㅋㅋ
잘 집중해서 따라올 수 있도록 해보자. 다음 시간에는 이를 Numpy로 표현하고 Pytorch와 비교해보도록 하겠다.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 9. 다중 분류 구현하기(심화실습) (2) | 2022.01.09 |
|---|---|
| 8. 다중 분류 구현하기(기초실습) (0) | 2022.01.09 |
| 6. 소프트맥스(softmax) 함수 탐구 (2) | 2022.01.07 |
| 5. 로지스틱 회귀 구현하기(실습) (0) | 2022.01.04 |
| 4. 로지스틱 회귀 구현하기(이론) (2) | 2022.01.04 |



