이전 시간에 로지스틱 회귀의 정의, 도함수를 유도하였다.
1. 복습
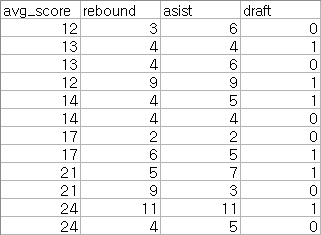
위 데이터는 평균 득점(avg_score), 리바운드 횟수(rebound), 어시스트 횟수(asist)에 따른 신인 농구 선수의 NBA 드래프트 여부 (1:성공, 0:실패) 이다. 이를 로지스틱 회귀로 예측할 것이다.
1) g(W, B) 연산은 아래와 같이 정의하였다.
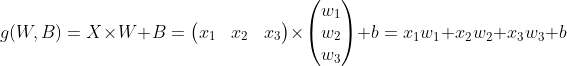
2) σ(g(W, B)) 연산은 아래와 같이 정의하였다.
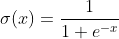
3) 순방향 연산 predict는 아래와 같이 최종 정의하였다.

4) 오차함수로 이진 교차 엔트로피 오차를 정의하였다.
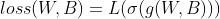

5) ∂loss(W,B) / ∂W 는 아래와 같이 정의하였다.
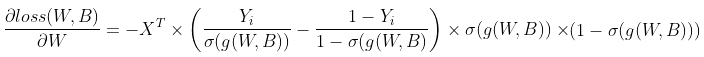
6) ∂loss(W,B) / ∂B 는 아래와 같이 정의하였다.
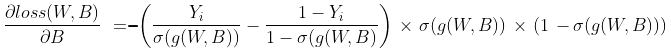
2. 데이터 준비하기
첨부파일을 받아 임포트한다. 데이터를 분할하고 weight W, bias B, learning_rate를 정의한다.
import numpy as np
from numpy import genfromtxt
np.random.seed(220104)
data = genfromtxt('NBA_Rookie_draft.csv', delimiter=',', skip_header = 1)
input = data[:, 0:3]
target = data[:, -1:]
W = np.random.randn(3, 1) # [[-0.30356914], [-0.56552733], [-0.44174438]]
B = np.random.randn(1, 1) # [[0.01214057]]
learning_rate = 0.001
3. 순방향 계산 정의하기
이전 시간에 언급했듯이, 로그는 자연로그(ln)을 사용하겠다.
def logistic_forward(X, Y, W, B):
XWB = np.dot(X, W) + B
pred = 1 / (1 + np.exp(-XWB))
# np.log()는 자연로그(ln)임
loss = np.sum(-Y*np.log(pred) - (1-Y)*np.log(1-pred))
return pred, loss
4. 오차함수 도함수 계산하기
def loss_gradient(X, Y, W, B):
# g(W, B)
XWB = np.dot(X, W) + B
# σ(g(W, B))
pred = 1 / (1 + np.exp(-XWB))
# ∂L(σ(g(W,B))) / ∂σ(g(W,B))
dL_dsig = -1*( (Y / pred) - ( (1-Y) / (1-pred) ) )
# ∂σ(g(W,B)) / ∂g(W,B)
dsig_dg = ( 1/(1+np.exp(-XWB)) ) * ( 1 - 1/(1+np.exp(-XWB)) )
# ∂g(W,B) / ∂W
dg_dW = np.transpose(X, (1, 0))
# ∂g(W,B) / ∂B = 1
#∂L(σ(g(W,B))) / ∂W
dloss_dW = np.dot(dg_dW, dL_dsig*dsig_dg)
#∂L(σ(g(W,B))) / ∂B
dloss_dB = np.sum(dL_dsig*dsig_dg, axis=0)
return dloss_dW, dloss_dB마지막 도함수 ∂loss/∂dB 구하기에서 ∂L/∂σ, ∂σ/∂g계산 결과는 각각 (batch, 1)이다. B는 (1, 1) 이므로 올바르게 계산하기 위해서는 더해주어야(np.sum)한다.
5. 학습 전 순방향과 W, B 알아보기
pred, loss = logistic_forward(input, target, W, B)
print('before pred', pred)
print('before loss', loss)
print('before W', W)
print('before B', B)
"""
before pred [[3.42897023e-04]
[3.47866051e-04]
[1.43815731e-04]
[3.06293296e-06]
[1.65122358e-04]
[2.56810750e-04]
[7.74066592e-04]
[2.14359275e-05]
[4.63134430e-06]
[2.82276579e-06]
[1.06948052e-08]
[7.93396201e-06]]
before loss 70.75679650741478
before W [[-0.30356914]
[-0.56552733]
[-0.44174438]]
before B [[0.01214057]]
"""학습전 예측값 pred, 오차 loss, weight W, bias B 를 주목하길 바란다. 의미가 없는 값들이다.
6. 경사하강법으로 학습하기
3000번 학습하였는데 과적합으로 인해 좋지 않다. 그러나 이번 예시에서는 조금 더 명확하게 보여주고자 많이 학습하였다.
for i in range(3000):
dL_dW, dL_dB = loss_gradient(input, target, W , B)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
7. 결과 확인하기
pred, loss = logistic_forward(input, target, W, B)
print('after pred', pred)
print('after loss', loss)
print('after W', W)
print('after B', B)
"""
after pred [[0.63286497]
[0.45883071]
[0.6644647 ]
[0.97888304]
[0.51531288]
[0.4102621 ]
[0.07742938]
[0.53516532]
[0.46538451]
[0.38011478]
[0.95183613]
[0.12819188]]
after loss 6.220960326814549
after W [[-0.19783118]
[ 0.33655838]
[ 0.42415269]]
after B [[-0.63608971]]
"""
| No. | avg_score | rebound | asist | draft | pred(Numpy) |
| 1 | 12 | 3 | 6 | 0 | 0.63286497 |
| 2 | 13 | 4 | 4 | 1 | 0.45883071 |
| 3 | 13 | 4 | 6 | 0 | 0.6644647 |
| 4 | 12 | 9 | 9 | 1 | 0.9788304 |
| 5 | 14 | 4 | 5 | 1 | 0.51531288 |
| 6 | 14 | 4 | 4 | 0 | 0.4102621 |
| 7 | 17 | 2 | 2 | 0 | 0.07742938 |
| 8 | 17 | 6 | 5 | 1 | 0.53516532 |
| 9 | 21 | 5 | 7 | 1 | 0.46538451 |
| 10 | 21 | 9 | 3 | 0 | 0.38011478 |
| 11 | 24 | 11 | 11 | 1 | 0.95183613 |
| 12 | 24 | 4 | 5 | 0 | 0.12819188 |
0에 가까울 수록 드래프트 실패, 1에 가까울 수록 드래프트 성공 으로 예측한 것이다. 맞는 것도 있지만 맞지 않는 것도 많다는 것을 알 수 있다. 확률 기반임에 유의하자.
잘못 예측한 편은 빨간색, 잘 예측한 편은 파란색으로 음영처리하였고 음영처리 하지 않은 것은 애매한 것으로 판단하였다.
히트맵 등으로 데이터 분석을 해 보면 좋은데 데이터 분석은 시간이 될 때 다루어 보겠다.
중요한 것은 평균 점수인 avg_score보다 rebound와 asist가 큰 영향을 미치는 것으로 보인다는 것이다. weight과 bias를 보면 알 수 있는데
after W [[-0.19783118]
[ 0.33655838]
[ 0.42415269]]
after B [[-0.63608971]]
W의 첫 번재 항은 avg_score 즉 평균 점수인데 -0.197.. 이라는 뜻은 평균점수는 중요하지 않다는 것으로 판단한 것이다.
0.33... 은 rebound, 0.424...은 asist인데 asist가 가장 크므로 asist를 가장 중요하게 판단했다는 것이다.
뭔가 이상하다고 느낄 수 있다. 당연하다. 여러 이유가 있는데
1) 데이터 수가 너무 적다.
2) 가중치 수가 적다
3) 정확하게 예측한다고 좋은 것이 아니다. 과적합이 일어나면 소용이 없다.
아래는 전체 코드이다.
import numpy as np
from numpy import genfromtxt
np.random.seed(220104)
data = genfromtxt('NBA_Rookie_draft.csv', delimiter=',', skip_header = 1)
input = data[:, 0:3]
target = data[:, -1:]
W = np.random.randn(3, 1) # [[-0.30356914], [-0.56552733], [-0.44174438]]
B = np.random.randn(1, 1) # [[0.01214057]]
learning_rate = 0.001
def logistic_forward(X, Y, W, B):
XWB = np.dot(X, W) + B
pred = 1 / (1 + np.exp(-XWB))
# np.log()는 자연로그(ln)임
loss = np.sum(-Y*np.log(pred) - (1-Y)*np.log(1-pred))
return pred, loss
def loss_gradient(X, Y, W, B):
# g(W, B)
XWB = np.dot(X, W) + B
# σ(g(W, B))
pred = 1 / (1 + np.exp(-XWB))
# ∂L(σ(g(W,B))) / ∂σ(g(W,B))
dL_dsig = -1*( (Y / pred) - ( (1-Y) / (1-pred) ) )
# ∂σ(g(W,B)) / ∂g(W,B)
dsig_dg = ( 1/(1+np.exp(-XWB)) ) * ( 1 - 1/(1+np.exp(-XWB)) )
# ∂g(W,B) / ∂W
dg_dW = np.transpose(X, (1, 0))
# ∂g(W,B) / ∂B = 1
#∂L(σ(g(W,B))) / ∂W
dloss_dW = np.dot(dg_dW, dL_dsig*dsig_dg)
#∂L(σ(g(W,B))) / ∂B
dloss_dB = np.sum(dL_dsig*dsig_dg, axis=0)
return dloss_dW, dloss_dB
pred, loss = logistic_forward(input, target, W, B)
"""
print('before pred', pred)
print('before loss', loss)
print('before W', W)
print('before B', B)
efore pred [[3.42897023e-04]
[3.47866051e-04]
[1.43815731e-04]
[3.06293296e-06]
[1.65122358e-04]
[2.56810750e-04]
[7.74066592e-04]
[2.14359275e-05]
[4.63134430e-06]
[2.82276579e-06]
[1.06948052e-08]
[7.93396201e-06]]
before loss 70.75679650741478
before W [[-0.30356914]
[-0.56552733]
[-0.44174438]]
before B [[0.01214057]]
"""
for i in range(3000):
dL_dW, dL_dB = loss_gradient(input, target, W , B)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
pred, loss = logistic_forward(input, target, W, B)
print('after pred', pred)
print('after loss', loss)
print('after W', W)
print('after B', B)
"""
after pred [[0.63286497]
[0.45883071]
[0.6644647 ]
[0.97888304]
[0.51531288]
[0.4102621 ]
[0.07742938]
[0.53516532]
[0.46538451]
[0.38011478]
[0.95183613]
[0.12819188]]
after loss 6.220960326814549
after W [[-0.19783118]
[ 0.33655838]
[ 0.42415269]]
after B [[-0.63608971]]
"""
8. pytorch로 학습하기
pytorch로 학습하였는데 사실 별 차이가 없었다.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from numpy import genfromtxt
data = genfromtxt('NBA_Rookie_draft.csv', delimiter=',', skip_header = 1)
input = data[:, 0:3]
target = data[:, -1:]
input = torch.FloatTensor(input)
target = torch.FloatTensor(target)
model = nn.Sequential(
nn.Linear(3, 1),
nn.Sigmoid()
)
"""
print(model(input))
tensor([[0.1699],
[0.0752],
[0.1071],
[0.0430],
[0.0759],
[0.0634],
[0.0505],
[0.0230],
[0.0230],
[0.0027],
[0.0036],
[0.0129]], grad_fn=<SigmoidBackward>)
"""
optimizer = optim.SGD(model.parameters(), lr=0.001)
epoches = 3000
for epoche in range(epoches + 1):
pred = model(input)
loss = F.binary_cross_entropy(pred, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
"""
print(model(input))
print(list(model.parameters()))
tensor([[0.6190],
[0.4700],
[0.6437],
[0.9617],
[0.5159],
[0.4275],
[0.1114],
[0.5260],
[0.4625],
[0.3869],
[0.9188],
[0.1602]], grad_fn=<SigmoidBackward>)
[Parameter containing:
tensor([[-0.1720, 0.2783, 0.3558]], requires_grad=True), Parameter containing:
tensor([-0.4204], requires_grad=True)]
"""
| No. | avg_score | rebound | asist | draft | pred(Numpy) | pred(Pytorch) |
| 1 | 12 | 3 | 6 | 0 | 0.63286497 | 0.619 |
| 2 | 13 | 4 | 4 | 1 | 0.45883071 | 0.47 |
| 3 | 13 | 4 | 6 | 0 | 0.6644647 | 0.6437 |
| 4 | 12 | 9 | 9 | 1 | 0.9788304 | 0.9617 |
| 5 | 14 | 4 | 5 | 1 | 0.51531288 | 0.5159 |
| 6 | 14 | 4 | 4 | 0 | 0.4102621 | 0.4275 |
| 7 | 17 | 2 | 2 | 0 | 0.07742938 | 0.1114 |
| 8 | 17 | 6 | 5 | 1 | 0.53516532 | 0.526 |
| 9 | 21 | 5 | 7 | 1 | 0.46538451 | 0.4625 |
| 10 | 21 | 9 | 3 | 0 | 0.38011478 | 0.3869 |
| 11 | 24 | 11 | 11 | 1 | 0.95183613 | 0.9188 |
| 12 | 24 | 4 | 5 | 0 | 0.12819188 | 0.1602 |
다음 시간에는 소프트맥스 회귀를 진행해 보겠다.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 7. 다중 분류 구현하기(이론) (0) | 2022.01.08 |
|---|---|
| 6. 소프트맥스(softmax) 함수 탐구 (2) | 2022.01.07 |
| 4. 로지스틱 회귀 구현하기(이론) (2) | 2022.01.04 |
| 3. 입력 특성이 2개인 선형회귀 구현(이론, 실습) (0) | 2022.01.03 |
| 2. 선형회귀 구현하기(실습) (0) | 2022.01.03 |



