로지스틱 회귀(logistic regression)은 선형결합으로 이루어진 모델(Y = WX + B)을 이용하여 어떤 사건을 분류하거나 예측하는데 사용한다.
단순 이진 분류인 경우 1, 0으로 분류되는데 선형회귀를 사용한다면 안전성이나 예측성공이 떨어진다.
새로운 데이터가 추가되면 직선 그래프(선형회귀 모델)를 크게 수정해야 하기 때문이다.

정확하게 1이다, 0이다 구별하는 대신, 1일 확률이 몇 %이다 라고 하는 것이 더 수월하고 이를 기반으로 한 모델은 데이터 추가나 변화에 유연성을 가진다. 이러한 성질을 가진 시그모이드 함수(sigmoid)를 많이 사용한다.
1. 로지스틱 회귀 데이터

위 데이터는 평균 득점(avg_score), 리바운드 횟수(rebound), 어시스트 횟수(asist)에 따른 신인 농구 선수의 NBA 드래프트 여부 (1:성공, 0:실패) 이다.
위 데이터를 입력 받고 드래프트 여부를 1, 0으로 예측하는 로지스틱 회귀 모델을 만들고자 한다.
2. 데이터 설정하기
입력 데이터의 특성(feature)는 avg_score, rebound, asist로 3개 → (1, 3)
목표 데이터의 특성은 1개(1 : 성공, 0 : 실패) → (1, 1)
Y = XW + B에 따라 weight matrix W는 (3, 1) , bias matrix B는 (1, 1) 이 되어야 할 것이다.
3. 순방향 연산(forward) → pred
1) g(W, B) 연산은 아래와 같이 정의한다.

2) σ(g(W, B)) 연산은 아래와 같이 정의한다.

따라서 순방향 연산 predict는 아래와 같이 최종 정의할 수 있다.

4. 오차함수
천천히 생각해보자.
정답은 1(또는 0)인데 predict(W, B) = 0(또는 1) 이라면 오차는 클 것이고
정답은 1(또는 0)인데 predict(W, B) = 1(또는 0) 이라면 오차는 작을 것이다.
그리고 이 오차함수는 경사하강법을 적용하기 위해 미분이 가능해야 한다!!!
이 오차함수에 대해 적절한 함수는 log 함수이다. 아래 그래프를 보자.
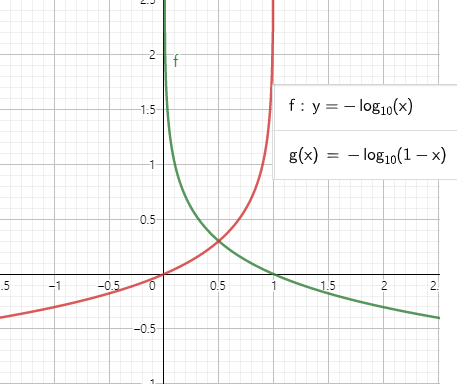
1) -log(x) 함수

x -> 0일 때 ∞ 으로 발산하고, x -> 1일 때 0으로 수렴한다.
목표값이 1일 때 모델이 0을 예측하면 오차를 크게, 모델이 1을 예측하면 오차는 0으로 사용할 수 있다.
2) -log(1-x) 함수

x -> 0일 때 0으로 수렴하고, x -> 1일 때 ∞ 으로 발산한다.
목표값이 0일 때 모델이 1을 예측하면 오차를 크게, 모델이 0을 예측하면 오차는 0으로 사용할 수 있다.
정답은 1(또는 0)인데 predict(W, B) = 0(또는 1) 이라면 오차는 클 것이고
정답은 1(또는 0)인데 predict(W, B) = 1(또는 0) 이라면 오차는 작을 것이다.
위에 언급한 것을 위의 두 함수와 연관짓는다면 오차함수로 사용하는 것은 타당하다.
즉, 이 두함수를 합치면 우리가 원하는 오차함수를 만들 수 있다.
5. 이진 교차 엔트로피 오차 함수(Binary Cross Entropy Error), BCEE
이진 교차 엔트로피 오차 함수(BCEE)는 아래와 같이 정의한다. 여기서는 loss(W, B)로 정의할 것이다.


1) 목표값 Y가 1일 때
σ(g(W, B)) = 0 또는 σ(g(W, B)) = 1을 대입
2) 목표값 Y가 1일 때
σ(g(W, B)) = 0 또는 σ(g(W, B)) = 1을 대입
하여 loss(W, B)값이 어떻게 변하는지 스스로 계산해 보자.
Y가 0( 또는 1) 일 때 σ(g(W, B))가 0( 또는 1) 이라면 loss(W, B) 값은 0에 가까울 것이고
Y가 1( 또는 0) 일 때 σ(g(W, B))가 0( 또는 1) 이라면 loss(W, B) 값은 ∞에 가까울 것이다.
이렇게 계산된다면 오차함수는 올바르게 설정한 것이다.
6. 도함수 구하기
W, B에 대한 오차함수 loss(W, B)의 도함수는 체인룰을 사용하면 아래와 같다.


1) ∂L(σ(g(W, B))) / ∂σ(g(W, B)) 은 log값을 미분해야 하는데 log 미분 성질을 이용하면 아래와 같다.
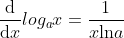


만약 a가 오일러 수 e 라면 ln(e) = 1이 되어 계산이 깔끔해 질 것이다. 코드는 이렇게 작성하겠다.
2) ∂σ(g(W, B)) / ∂g(W, B) 은 아래와 같다.

3) ∂g(W, B) / ∂W 은 아래와 같다.

4) ∂g(W, B) / ∂B 는 아래와 같다.

5) 위 내용을 종합하면 ∂loss(W,B) / ∂W 는 아래와 같다.

6) ∂loss(W,B) / ∂B 는 아래와 같다.

모든 준비는 끝났다. 다음 이론에서는 코드로 직접 구현해 보고 pytorch로 검증할 것이다.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 6. 소프트맥스(softmax) 함수 탐구 (2) | 2022.01.07 |
|---|---|
| 5. 로지스틱 회귀 구현하기(실습) (0) | 2022.01.04 |
| 3. 입력 특성이 2개인 선형회귀 구현(이론, 실습) (0) | 2022.01.03 |
| 2. 선형회귀 구현하기(실습) (0) | 2022.01.03 |
| 1. 선형회귀 구현하기(이론) (0) | 2022.01.03 |



