소프트맥스(softmax)함수는 딥러닝에서 다중 분류에 쓰이는데 오늘은 그 유래, 정의, 장점과 단점을 다루고자 한다.
1. 유래
학부과정 물리학을 공부하다 보면 열 및 통계물리(줄여서 통계물리)를 공부할 때가 온다.(본인은 미천한 물리 학사임)
통상적으로 기체는 수 많은 입자들로 구성되어 있는데 (기본 10^(23)개) 입자들 각각에 대한 운동 방정식을 세우는 것은 불가능에 가깝다.
따라서 미시세계의 입자 운동을 통계적으로 분석하는 것이 통계물리이다. 통계물리의 아버지라 물리는 루드비히 볼츠만이 대표적인 물리학자이다. (개인적으로 아인슈타인, 파인만보다 더 천재적이라고 생각한다.)

볼츠만 전기로 가장 유명한 '볼츠만의 원자' 라는 책이 있다. 과학에 관심이 많은 학생부터 어른까지 물리학을 공부한다면 두번 읽어라 세번 읽어라

어려운 통계물리를 계속 공부하다 보면 통계물리에서 가장 중요한 볼츠만 인자와 볼츠만 통계에 도달하게 된다.
볼츠만 인자(boltzmann factor)

여기서 E(s)는 어떤 상태 s일 때 입자의 에너지, k는 볼츠만 상수, T는 열평형 상태에서의 온도이다.
여기서부터 정말 중요한 내용인데, 어떤 상태 s에서 에너지 E(s)를 가지는 입자를 발견할 확률( P(s) )은 다음과 같이 구할 수 있다.

어떤 입자를 모든 상태에서 발견한 확률은 1이여야 하므로

뭔 소리인지 모를 수 있다. 당연하다. 난 딥러닝을 배우러 왔는데 왜 물리학이 나오지? 생각이 든다. 그래서 구체적인 설명은 한도 끝도 없으므로 거두절미하고 핵심만 이야기하겠다.

이 식은 온도 T인 열평형 계에서 상태 s에 있는 입자를 발견할 확률을 의미한다. -> 입자를 발견할 확률을 의미한다.
위 식은 많은 과학 분야에서 사용되다가 1959년 Robert Duncan Luce는 자신의 책 Individual Choice Behavor: A Theoretical Analysis에서 기계학습에 소프트맥스로 알려진 위 식을 사용할 것을 제안하였다. 1989년 Hohn S. Bridle은 비선형성 네트워크 출력을 확률로 처리하고자 소프트맥스 사용을 제안하였다.
2. 정의(쉽게 쉽게...)
예를 들어 보자. 임의의 학생 집단을 초등학생(es), 중학생(ms), 고등학생(hs)으로 분류하는 문제가 있다. 3개의 집단이다. 어떤 학생 x가 초등학생, 중학생, 고등학생 집단에 속할 확률은 각각 아래와 같다.

(볼츠만 분포, 분배함수와 매우 비슷하다. )
자세한 정의는 이것보다 더 좋은 유튜브 강의들을 보시길...
3. 장점
소프트맥스 함수를 쓰는 이유가 있지 않을까? 첫 번째로 지수함수의 특성상 값이 크게 변한다는 것이 있는데 값이 조금만 변하여도 출력은 크게 변한다. 예를 들어 보자.
학생으로 이루어진 집단 A가 있다. 이 집단은 초등학생 1명, 중학생 1명, 고등학생 3명으로 (초등학생 수, 중학생 수, 고등학생 수) -> A(1, 1, 3)인 집단이다. 이 중 임의로 한명을 콕 집었을 때 그 학생이 초등학생, 중학생, 고등학생일 확률을 각각 구해보자.
초등학생 수 es, 중학생 수 ms, 고등학생 수를 hs 라고 하자.
1) 일반적인 확률 개념으로 생각해 보면 확률 = 어떤 집단일 경우의 수 / 모든 경우의 수 로 표현할 수 있지 않은가?
이를 이용해 보면
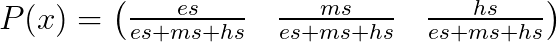

2) 소프트맥스로 표현해 보면
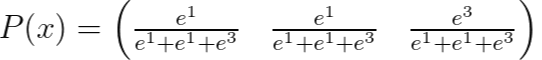
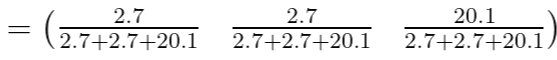
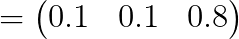
여기서 알 수 있는 사실은 큰 값의 가중치를 크게 부여한다는 것이다. (0.6에서 0.8로 가중치 부여)
또한 값을 변화시켰을 때도 소프트맥스에서 더 두드러지게 표현된다. (값을 1 정도 변화시켜 보고 직접 계산해 보자.)
4. 단점
값이 지수함수적으로 변화하다 보니까 너무 커지는 바람에 overflow문제가 자주 발생한다. 값이 너무 켜져서 컴퓨터가 계산할 수 없다는 뜻이다. Numpy로 다중 분류 문제를 짤 텐데 learning rate를 잘못 설정하면 경사하강법 적용 중에 overflow가 생각보다 많이 목격된다. (nan 으로 표시됨) 보다 세심한 설정이 필요하다.
다음시간에는 소프트맥스를 이용하여 다중 분류 문제를 어떻게 학습할 수 있는지 보여줄 것이다.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 8. 다중 분류 구현하기(기초실습) (0) | 2022.01.09 |
|---|---|
| 7. 다중 분류 구현하기(이론) (0) | 2022.01.08 |
| 5. 로지스틱 회귀 구현하기(실습) (0) | 2022.01.04 |
| 4. 로지스틱 회귀 구현하기(이론) (2) | 2022.01.04 |
| 3. 입력 특성이 2개인 선형회귀 구현(이론, 실습) (0) | 2022.01.03 |



