본문 바로가기
파이썬 프로그래밍/Numpy 딥러닝

8. 다중 분류 구현하기(기초실습)

by Majestyblue 2022. 1. 9.

이전시간에 소프트맥스, 크로스엔트로피를 이용하여 아이리스 꽃 분류 문제를 어떻게 해결할 수 있는지 이론적으로 알아보았다. 이번엔 단 한개의 데이터를 이용하여 이론을 넘파이 코드로 작성하고 pytorch와 비교해보는 시간을 갖도록 하겠다.

 

1. 데이터 정의

입력 input, 목표값 target, 가중치 W, 편향 B, 학습률 learning_rate를 정의한다.

import numpy as np

np.random.seed(220106)
input = np.array([[1.2, 2.4, 3.6, 1.8]], dtype=np.float32)

target = np.array([[0, 0, 1]], dtype=np.int32)

W = np.random.randn(3, 4)
B  = np.random.randn(3, 1)

learning_rate = 0.001

 

2. 순방향 연산 정의

 

 

 

위의 수식에 따라 WX + B 연산을 실시한다. X를 전치시킨 것에 주목해 보자.

X = np.transpose(X, (1, 0))
WXB = np.dot(W, X) + B

 

 

이 식을 소프트맥스에 통과시키기 위해 각 값에 지수를 씌운다.

    e_WXB1 = np.exp(WXB[0])
    e_WXB2 = np.exp(WXB[1])
    e_WXB3 = np.exp(WXB[2])

 

 

아래처럼 소프트맥스 함수를 코드로 정의한다.

 

 

 

    sum_e_WXB = e_WXB1 + e_WXB2 + e_WXB3
    
    smax_WXB1 = e_WXB1 / sum_e_WXB
    smax_WXB2 = e_WXB2 / sum_e_WXB
    smax_WXB3 = e_WXB3 / sum_e_WXB
    
    pred = np.array([[smax_WXB1[0], smax_WXB2[0], smax_WXB3[0]]])

 

 

 

3. 오차 구하기

 

pred 값에서 타겟값만 고르기 위해 요소곱을 수행한다.

 

아래 식에서 Y= [0, 0, 1] 이므로 pred 행렬에서 smax_WXB1, smax_WXB2 값은 0과 곱하게 되어 사라지고 smax_WXB3 만 남게 된다. 이 값을 Y_target 이라고 정의하였고 여기에 -log 한 것이 오차(loss)가 된다.

 

    Y_target = np.sum(pred * Y, axis = 1, keepdims=True)
    
    loss = -np.log(Y_target)

 

 

4. 도함수 구하기(backward)

도함수 구하는 과정은 backward 연산이다. 체인룰을 통해 출력부터 거꾸로 탐색해서 들어간다. 

 

 

1) ∂loss(W,B)/∂W 의 정의와 결과값은 각각 아래와 같았다.

 

dloss(W,B) / dW 도함수의 체인룰

 

dloss(W,B) / dW 도함수의 결과값

 

 

∂L/∂S 는 S(g(W,B)) 값을 -1로 나누면 된다.

    #∂L(smax(g(W, B))) / ∂smax(g(W,B))
    dL_dsmax = -1 / Y_target[0][0]

 

 

∂S/∂g 는 softmax 도함수 행렬(3X3)에 Y값을 전치하여 행렬곱 해주면 된다.

(여기서 Y는 이미 전치되었다. 전체 코드에서 다시 확인할 수 있다.)

    #smax 도함수 행렬(3x3) 
    dsmax_dg_matrix = np.array([[(smax_WXB1*(1-smax_WXB1))[0], -(smax_WXB1*smax_WXB2)[0], -(smax_WXB1*smax_WXB3)[0]], 
                                [-(smax_WXB1*smax_WXB2)[0], (smax_WXB2*(1-smax_WXB1))[0], -(smax_WXB2*smax_WXB3)[0]],
                                [-(smax_WXB1*smax_WXB3)[0], -(smax_WXB2*smax_WXB3)[0], (smax_WXB2*(1-smax_WXB1))[0]]])
    
    #∂smax(g(W, B)) / ∂g(W,B) -> smax 도함수 행렬(3x3)에 target Y를 곱하여 해당 값 추출
	dsmax_dg = np.dot(dsmax_dg_matrix, np.transpose(Y, (1, 0)))

 

∂g/∂W 는 X의 전치행렬이였다. g(W,B) 연산 들어가기 전에 X를 전치했었고, 다시 전치하는 것이므로 원래의 shape으로 돌아가는 것에 유의하자.

 

    #∂g(W, B) / ∂W
    dg_dW = np.transpose(X, (1, 0))

 

최종 ∂loss(W,B)/∂W 은 위에 구한 셋을 곱해주면 되는데 ∂L/∂S는 스칼라이므로 스칼라곱을 하고 ∂S/∂g과 ∂g/∂W는 각각 (3, 1), (1, 4)의 행렬이므로 행렬곱을 해주면 (3, 4)의 W의 shape과 동일한 도함수 행렬이 나온다.

 

    #∂loss(W,B) / ∂W
    dloss_dW = dL_dsmax*np.dot(dsmax_dg, dg_dW)

 

 

 

 

 

2) ∂loss(W,B)/∂B 의 정의와 결과값은 아래와 같았다.

 

dloss(W,B) / dB 도함수의 체인룰

 

dloss(W,B) / dB 도함수의 결과값

 

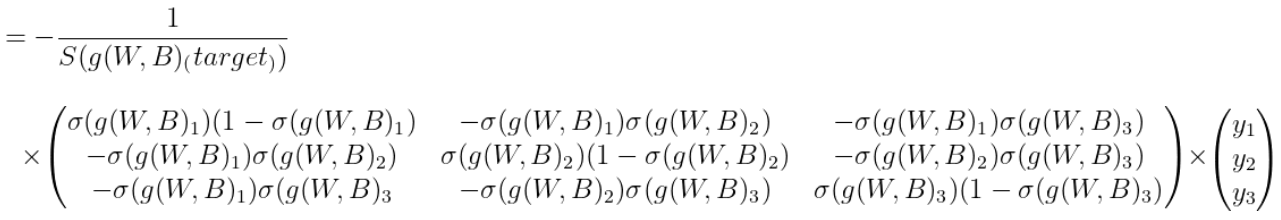
∂L/∂S, ∂S/∂g는 위와 동일하고 ∂g/∂B는 (3, 1) shape의 요소 1로 이루어진 행렬이였다. 따라서 ∂L/∂S, ∂S/∂g을 서로 행렬곱하면 구할 수 있다.

 

    #∂loss(W,B) / ∂B
    dloss_dB = dL_dsmax*dsmax_dg

 

 

 

5. 훈련하기

한 개의 데이터라 100회 훈련하였다. learning_rate = 0.001이다. 크면 overflow 발생한다. 기울기를 구하고 경사하강법으로 weight와 bias를 업데이트한다.

for i in range(100): 
    dL_dW, dL_dB = loss_gradient(input, target, W , B) 
    W = W + -1*learning_rate * dL_dW 
    B = B + -1*learning_rate * dL_dB

 

 

 

6. 결과 확인하기

 

1) 훈련 전

pred, loss = softmax_forward(input, target, W, B)
print('before pred', pred) 
print('before loss', loss) 
print('before W', W) 
print('before B', B)
"""
before pred [[0.42185561 0.4060726  0.17207179]]
before loss [[1.7598435]]
before W [[ 0.77008731 -1.62624216  0.65101361 -1.09693664]
 [-0.23589309 -0.66088299 -0.06840472 -0.26426033]
 [ 0.84554461 -0.78046195 -0.56530934 -1.00184115]]
before B [[1.03851627]
 [0.98178811]
 [2.22893421]]
"""

훈련 전 pred 예측값을 보면 각 확률이 약 (0.43, 0.4, 0.17)으로 되어 있다. 정답은 (0, 0, 1) 이므로 세 번째 0.17의 확률이 증가해야 한다. 훈련을 하고 결과를 확인해 보면 아래와 같다.

 

 

 

2) 훈련 후

pred, loss = softmax_forward(input, target, W, B)
print('after pred', pred) 
print('after loss', loss) 
print('after W', W) 
print('after B', B)
"""
after pred [[0.19477982 0.19114482 0.61407536]]
after loss [[0.48763762]]
after W [[ 0.73505999 -1.6962968   0.54593166 -1.14947762]
 [-0.26997158 -0.72903998 -0.17064019 -0.31537807]
 [ 0.91109103 -0.64936912 -0.3686701  -0.90352153]]
after B [[1.00932684]
 [0.95338937]
 [2.28355623]]
"""

100회 훈련하였을 때 pred 예측값이 순서대로 약 (0.20, 0.19, 0.61) 로 0.17에서 0.61로 증가한 것을 볼 수 있고 나머지는 감소한 것을 확인할 수 있다. 

 

전체 코드이다.

import numpy as np

np.random.seed(220106)
input = np.array([[1.2, 2.4, 3.6, 1.8]], dtype=np.float32)

target = np.array([[0, 0, 1]], dtype=np.int32)

W = np.random.randn(3, 4)
B  = np.random.randn(3, 1)

learning_rate = 0.001

def softmax_forward(X, Y, W, B):
    # preprocessing data for calculate
    X = np.transpose(X, (1, 0))
    WXB = np.dot(W, X) + B 
    
    e_WXB1 = np.exp(WXB[0])
    e_WXB2 = np.exp(WXB[1])
    e_WXB3 = np.exp(WXB[2])
    
    sum_e_WXB = e_WXB1 + e_WXB2 + e_WXB3
    
    smax_WXB1 = e_WXB1 / sum_e_WXB
    smax_WXB2 = e_WXB2 / sum_e_WXB
    smax_WXB3 = e_WXB3 / sum_e_WXB
    
    pred = np.array([[smax_WXB1[0], smax_WXB2[0], smax_WXB3[0]]])
    
    Y_target = np.sum(pred * Y, axis = 1, keepdims=True)
    
    loss = -np.log(Y_target)
    
    return pred, loss
   


def loss_gradient(X, Y, W, B):
    # preprocessing data for calculate
    X = np.transpose(X, (1, 0))
    WXB = np.dot(W, X) + B 
    
    e_WXB1 = np.exp(WXB[0])
    e_WXB2 = np.exp(WXB[1])
    e_WXB3 = np.exp(WXB[2])
    
    sum_e_WXB = e_WXB1 + e_WXB2 + e_WXB3
    
    smax_WXB1 = e_WXB1 / sum_e_WXB
    smax_WXB2 = e_WXB2 / sum_e_WXB
    smax_WXB3 = e_WXB3 / sum_e_WXB
    
    softmax = np.array([[smax_WXB1[0], smax_WXB2[0], smax_WXB3[0]]])
    
    # Y가 1인 softxmax 출력만 남기기 위해 transpose를 하고 곱한다.
    
    Y_target = np.sum(softmax * Y, axis = 1, keepdims=True)
    
    #∂L(smax(g(W, B))) / ∂smax(g(W,B))
    dL_dsmax = -1 / Y_target[0][0]
    
    #smax 도함수 행렬(3x3) 
    dsmax_dg_matrix = np.array([[(smax_WXB1*(1-smax_WXB1))[0], -(smax_WXB1*smax_WXB2)[0], -(smax_WXB1*smax_WXB3)[0]], 
                                [-(smax_WXB1*smax_WXB2)[0], (smax_WXB2*(1-smax_WXB1))[0], -(smax_WXB2*smax_WXB3)[0]],
                                [-(smax_WXB1*smax_WXB3)[0], -(smax_WXB2*smax_WXB3)[0], (smax_WXB2*(1-smax_WXB1))[0]]])
    
    #∂smax(g(W, B)) / ∂g(W,B) -> smax 도함수 행렬(3x3)에 target Y를 곱하여 해당 값 추출
    dsmax_dg = np.dot(dsmax_dg_matrix, np.transpose(Y, (1, 0)))
    
    #∂g(W, B) / ∂W
    dg_dW = np.transpose(X, (1, 0))

    #∂loss(W,B) / ∂W
    dloss_dW = dL_dsmax*np.dot(dsmax_dg, dg_dW)
    
    #∂loss(W,B) / ∂B
    dloss_dB = dL_dsmax*dsmax_dg

    
    return dloss_dW, dloss_dB


pred, loss = softmax_forward(input, target, W, B)
print('before pred', pred) 
print('before loss', loss) 
"""
print('before W', W) 
print('before B', B)
before pred [[0.42185561 0.4060726  0.17207179]]
before loss [[1.7598435]]
before W [[ 0.77008731 -1.62624216  0.65101361 -1.09693664]
 [-0.23589309 -0.66088299 -0.06840472 -0.26426033]
 [ 0.84554461 -0.78046195 -0.56530934 -1.00184115]]
before B [[1.03851627]
 [0.98178811]
 [2.22893421]]
"""


for i in range(100): 
    dL_dW, dL_dB = loss_gradient(input, target, W , B) 
    W = W + -1*learning_rate * dL_dW 
    B = B + -1*learning_rate * dL_dB


pred, loss = softmax_forward(input, target, W, B)
print('after pred', pred) 
print('after loss', loss) 
"""
after pred [[0.19477982 0.19114482 0.61407536]]
after loss [[0.48763762]]
after W [[ 0.73505999 -1.6962968   0.54593166 -1.14947762]
 [-0.26997158 -0.72903998 -0.17064019 -0.31537807]
 [ 0.91109103 -0.64936912 -0.3686701  -0.90352153]]
after B [[1.00932684]
 [0.95338937]
 [2.28355623]]
print('after W', W) 
print('after B', B)
"""

 

사실 데이터 1개로는 의미가 없다. 실습을 2차시로 준비하게 되었냐면, 데이터 양이 증가하면 코드가 조금 까다로워지기 때문에 그걸 설명하고자 분리하였다. 다음 시간에 iris 꽃 데이터 중 30개만 추출한 csv 파일을 업로드하고 pytorch 연산과 비교해 보겠다.

저작자표시

'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글

10. 단층 퍼셉트론  (0) 2022.01.10
9. 다중 분류 구현하기(심화실습)  (2) 2022.01.09
7. 다중 분류 구현하기(이론)  (0) 2022.01.08
6. 소프트맥스(softmax) 함수 탐구  (2) 2022.01.07
5. 로지스틱 회귀 구현하기(실습)  (0) 2022.01.04

관련글

티스토리툴바