1969년 우리가 지금까지 사용한 단층 퍼셉트론은 XOR 문제를 해결할 수 없다고 증명되었다. 인공지능 연구 진척이 더뎌지기 시작했는데 도대체 무슨 일이 있었던 걸까
1. 논리게이트 (Logic gate)
논리게이트는 쉽게 말해 회로에서 사용되는 논리적 연산을 위한 전자도구이다. 이러한 논리적 전자 도구가 없었다면 우리는 다양한 전자기기들을 사용하지 못했을 것이다.
어떻게 작동하는지 궁금하다면 아래 동영상을 참고해 보길 바란다.
논리게이트는 입력 신호를 논리적 처리를 하고 출력한다. 아래 표는 입력에 따른 출력을 나타낸다.
이번 시간은 4가지, OR, AND, NAND, XOR을 이야기 해 보겠다.

0 : 입력 없음
1 : 입력 있음
위의 표를 보면서 확인하길 바란다.
OR 게이트 : 두 개의 입력 중 1개라도 있다면(1) 출력은 1, 하나라도 없으면 0이다.
AND 게이트 : 두 개의 입력 모두 있어야 출력은 1, 그 외에는 0이다.
NAND 게이트 : NOT AND의 약자로 AND 연산의 반대이다. 즉, 두 개의 입력 모두 있다면 0, 그 외에는 1이다.
XOR 게이트 : Exclusive OR의 약자로 상호 배재적인 연산이다. 두 입력같이 같으면 0, 다르면 1이다.
2. 퍼셉트론으로 논리게이트 만들기(OR 게이트 예시)
구현과 관련된 개념은 https://toyourlight.tistory.com/15 여기를 참고하길 바란다.
로지스틱 회귀를 이용하여 입력값에 따라 1과 0을 예측하게 할 것이다.
import numpy as np
np.random.seed(220111)
input = np.array([[0., 0.],
[1., 0.],
[0., 1.],
[1., 1.]], dtype = np.float32)
target_or = np.array([[0.],
[1.],
[1.],
[1.]], dtype = np.float32)
target_and = np.array([[0.],
[0.],
[0.],
[1.]], dtype = np.float32)
target_nand = np.array([[1.],
[1.],
[1.],
[0.]], dtype = np.float32)
target_xor = np.array([[0.],
[1.],
[1.],
[0.]], dtype = np.float32)
W = np.random.randn(2, 1) #[[ 0.90256913] [-0.03297993]]
B = np.random.randn(1, 1) # [[0.31467754]]
learning_rate = 1
def logistic_forward(X, Y, W, B):
XWB = np.dot(X, W) + B
pred = 1 / (1 + np.exp(-XWB))
loss = np.sum(-Y*np.log(pred) - (1-Y)*np.log(1-pred))
return pred, loss
def loss_gradient(X, Y, W, B):
XWB = np.dot(X, W) + B
pred = 1 / (1 + np.exp(-XWB))
dL_dsig = -1*( (Y / pred) - ( (1-Y) / (1-pred) ) )
dsig_dg = ( 1/(1+np.exp(-XWB)) ) * ( 1 - 1/(1+np.exp(-XWB)) )
dg_dW = np.transpose(X, (1, 0))
dloss_dW = np.dot(dg_dW, dL_dsig*dsig_dg)
dloss_dB = np.sum(dL_dsig*dsig_dg, axis=0)
return dloss_dW, dloss_dB
pred, loss = logistic_forward(input, target_or, W, B)
"""
before pred [[0.57802658]
[0.77157865]
[0.56996237]
[0.76571411]]
before loss 1.9512609799244536
before W [[ 0.90256913]
[-0.03297993]]
before B [[0.31467754]]
print('before pred', pred)
print('before loss', loss)
print('before W', W)
print('before B', B)
"""
for i in range(100):
dL_dW, dL_dB = loss_gradient(input, target_or, W , B)
W = W + -1*learning_rate * dL_dW
B = B + -1*learning_rate * dL_dB
pred, loss = logistic_forward(input, target_or, W, B)
"""
-----target or-----
print('after pred', pred)
print('after loss', loss)
print('after W', W)
print('after B', B)
after pred [[0.05054882]
[0.97990902]
[0.97982708]
[0.99997753]]
after loss 0.09256835755431797
after W [[6.8201335 ]
[6.81597938]]
after B [[-2.93294459]]
"""
"""
-----target and-----
print('after pred', pred)
print('after loss', loss)
print('after W', W)
print('after B', B)
after pred [[1.86891641e-04]
[4.82818309e-02]
[4.82805177e-02]
[9.32285504e-01]]
after loss 0.16927436389021555
after W [[5.60358103]
[5.60355245]]
after B [[-8.58479466]]
"""
"""
-----target nand-----
print('after pred', pred)
print('after loss', loss)
print('after W', W)
print('after B', B)
after pred [[0.9998086 ]
[0.95135604]
[0.951355 ]
[0.0682257 ]]
after loss 0.17059097646132404
after W [[-5.58760745]
[-5.58763005]]
after B [[8.5609682]]
"""
"""
-----target xor-----
print('after pred', pred)
print('after loss', loss)
print('after W', W)
print('after B', B)
after pred [[0.5]
[0.5]
[0.5]
[0.5]]
after loss 2.772588722239781
after W [[5.90580285e-09]
[5.90548144e-09]]
after B [[-7.0049222e-09]]
"""
1) 결과 분석
target_or은 원래 목표 값이고 pred는 훈련을 통해 순방향 연산에서 예측한 값이다. 잘 예측한 것을 알 수 있다.
| x1 | x2 | target_or | pred |
| 0 | 0 | 0 | 0.05 |
| 1 | 0 | 1 | 0.98 |
| 0 | 1 | 1 | 0.98 |
| 1 | 1 | 1 | 0.99 |
2) 시각적 분석
각 가중치 값과 선형 회귀식 z = X*W + B 의 식이다.
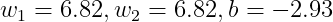

이 값을 3차원 그래프에 그려보면 아래의 평면 그래프가 나온다. z = ax + by + c 의 평면그래프인데 주목할 것은 Z가 양수인 경우와 음수인 경우이다. (Z가 음수라면 x, y 평면 아래에 있다.) 즉, 평면이 Z축에서 멀어질 수록 Z값은 양수이다.

Z > 0인 곳의 x1, x2 평면을 보면 요소가 (0, 1), (1, 0), (1, 1)가 포함되고 pred는 전부 1을 가리키고
Z < 0인 곳의 x1, x2 평면을 보면 요소가 (0, 0) 이고 pred는 0을 가리킨다.
왜냐하면
Z > 0 일 때 σ(z) → 1이고
Z < 0 일 때 σ(z) → 0이기 때문이다.
아래 시그모이드 함수 그래프를 보면서 값을 유추하길 바란다.

이를 z = 0인 2차원 표면에 1차원 직선으로 표현할 수 있는데 3차원 그래프에서의 결과를 생각해 보면
그래프 아래 구역은 pred가 0을 예측하고 그래프 윗 구역은 pred가 1을 예측한다.
즉, 그래프에서 위로 멀어지면 Z가 증가하는 방향이므로 시그모이드 함수 출력인 모델은 1을 크게 예측할 것이며
그래프에서 아래로 멀어지면 Z가 감소하는 방향이므로 시그모이드 함수 출력인 모델은 0을 크게 예측할 것이다.
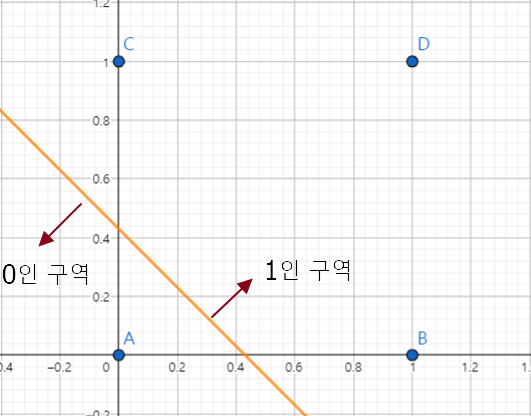
나머지 AND, NAND도 계산해 보길 바란다. 아래는 계산한 값을 토대로 그린 그래프이다.
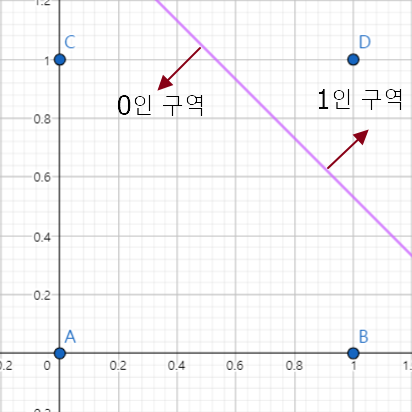
NAND 그래프를 3차원에 그리면 평면 기울기가 OR, AND과 반대이다. 즉 Z축에 가까울 수록 Z값은 양수이다.
따라서 z = 0 인 x1, x2 평면에서는 반대로 직선 위가 0, 직선 아래가 1이다.


3. 퍼셉트론으로 논리게이트 만들기(XOR 게이트)
결과를 확인해 보자.
| x1 | x2 | target_xor | pred |
| 0 | 0 | 0 | 0.5 |
| 1 | 0 | 1 | 0.5 |
| 0 | 1 | 1 | 0.5 |
| 1 | 1 | 0 | 0.5 |
after W [[5.90580285e-09] [5.90548144e-09]
after B [[-7.0049222e-09]]
가중치 값들은 0에 가깝다. 아래는 z값에 대한 3차원 그래프이다.
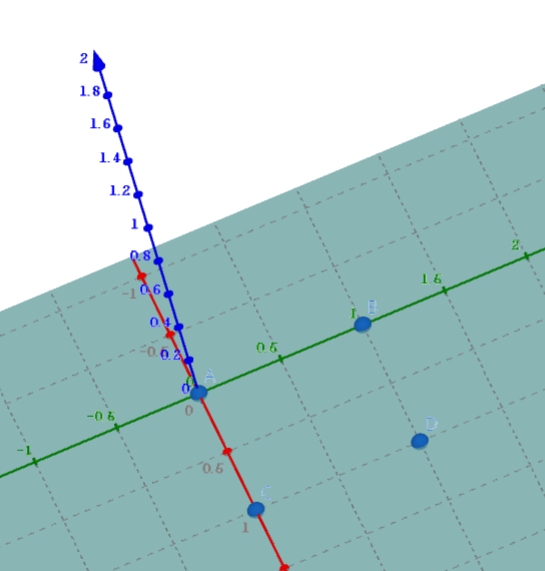
위의 3차원 그래프와 비교해 보면 알 수 있는데 평면이 z축에 나란하다. 즉, z = 0이라는 뜻인데 sigmoid 함수에서 z=0 이라면 1 / (1+e^(-0)) = 1 / (1 + 1) = 1 / 2 이다. 제대로 예측할 수 없다는 뜻이다.
XOR 문제는 오랫동안 인공지능 연구자들을 괴롭혀왔던 문제다. 단층 퍼셉트론으로 XOR 모델을 만들 수 없었다.
어떻게 해야 이 문제를 해결할 수 있을까?
다음 차시에서는 선형 회귀식의 한계를 알아보겠다.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 13. 다층 퍼셉트론(MPL) 등장 - 1.XOR 문제 해결(기초이론) (0) | 2022.01.18 |
|---|---|
| 12. 단층 퍼셉트론의 한계-2.선형 회귀식의 한계 (0) | 2022.01.12 |
| 10. 단층 퍼셉트론 (0) | 2022.01.10 |
| 9. 다중 분류 구현하기(심화실습) (2) | 2022.01.09 |
| 8. 다중 분류 구현하기(기초실습) (0) | 2022.01.09 |



