17. 다층 퍼셉트론(MPL)의 등장-2.비선형 회귀식(심화이론)

저번시간에 단순 선형회귀식의 한계를 확인하고 대책으로 비선형 회귀식을 제시하였다. 이를 위해 다층 퍼셉트론의 이용과 비선형함수로 시그모이드 대신 ReLU 함수를 사용할 것을 확인하였다.

 

순방향 전파는 아래와 같다. G는 선형연산(WX + B) 이고 R은 ReLU 함수이다.

 

 

이번 시간에는 순방향 전파, 역전파를 이용한 도함수를 구할 것이다. 

 

 

 

1. 데이터 정의

데이터는 아래와 같이 키, 몸무게를 이용할 것이다. '12. 단층 퍼셉트론의 한계-2.선형 회귀식의 한계' 에서 아래와 같은 데이터에서는 선형 회귀식으로 모델을 만들기 어렵다고 결론을 내렸었다.

 

몸무게(weight)에 따른 키(height)

 

초록색 선 pred2가 이차함수 형태의 선형회귀 모델

그야말로 총체적 난국이다 (...)

 

 

 

입력, 목표값, 가중치, 편향은 아래와 같다. shape을 유심히 보길 바란다.

1) 입력 : input (batch_size, 1)

2) 목표값 : target (batch_size, 1)

3) 가중치 및 편향

(1) G1 가중치 : W1 (8, 1) , G1 편향 : B1 (8, 1)

(2) G2 가중치 : W2 (4, 8) , G1 편향 : B2 (4, 1)

(3) G3 가중치 : W3 (1, 4) , G1 편향 : B3 (1, 1)

 

 

 

 

2.순방향 연산(forward)

 

1) G1연산은 아래와 같이 정의된다. 

 

 

 

 

 

2) R1연산은 아래와 같이 정의된다. 

 

 

 

 

 

3) G2연산은 아래와 같이 정의된다. 

 

 

 

 

4) R2연산은 아래와 같이 정의된다. 

 

 

 

 

5) G3연산은 아래와 같이 정의된다.

이 출력값이 모델 예측값인 Pred가 된다. G3 값에서 활성화함수를 통과하지 않는데 그 이유는 최종 값이 모델이 예측한 키(Height)이 되어야 하기 때문이다. 여기서 키(height) 값은 음수가 없기 때문에 ReLU를 활성화함수로 사용해도 괜찮지만 결과는 똑같으므로 사용하지 않는다.

 

 

 

 

 

6) 오차 함수는 평균 제곱 오차(MSE, Mean Square Error)를 사용한다.

(target shape(batch, 1)과 맞지 않기 때문에 pred를 전치(batch, 1)한다)

 

 

 

 

 

 

3. 역방향 연산(backward)

각 가중치에 대한 도함수는 다음과 같다.

 

 

 

 

 

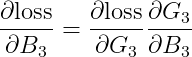
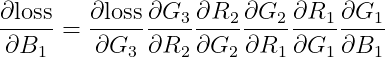
여기서 구해야 하는 도함수들은 대부분 Numpy 딥러닝 시리즈를 정주행하면 알 수 있는 것들이다. 아래는 대표적으로 구해야 하는 것을 수식화 한 것이다.

 

출력값(G3)에 대한 오차함수의 도함수

 

선형연산 G(i)에 대한 이전 활성화함수R(i-1) 도함수, 활성화함수 R(i)에 대한 선형연산 G(i)의 도함수

 

선형연산 G(i) = W(i)X(i) + B(i)에 대한 W(i)와 B(i)의 도함수

 

 

 

 

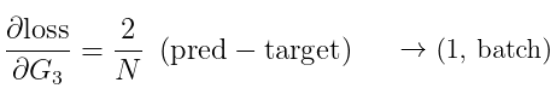
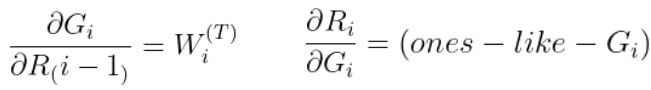
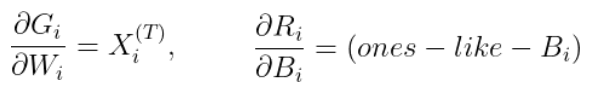
1) 오차함수에 대한 W3, B3의 도함수는 각각 아래와 같다.

 

 

 

 

 

 

 

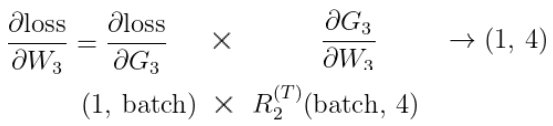
2) 오차함수에 대한 W2, B2의 도함수는 각각 아래와 같다.

 

 

 

 

 

3) 오차함수에 대한 W1, B1의 도함수는 각각 아래와 같다.

 

 

 

 

 

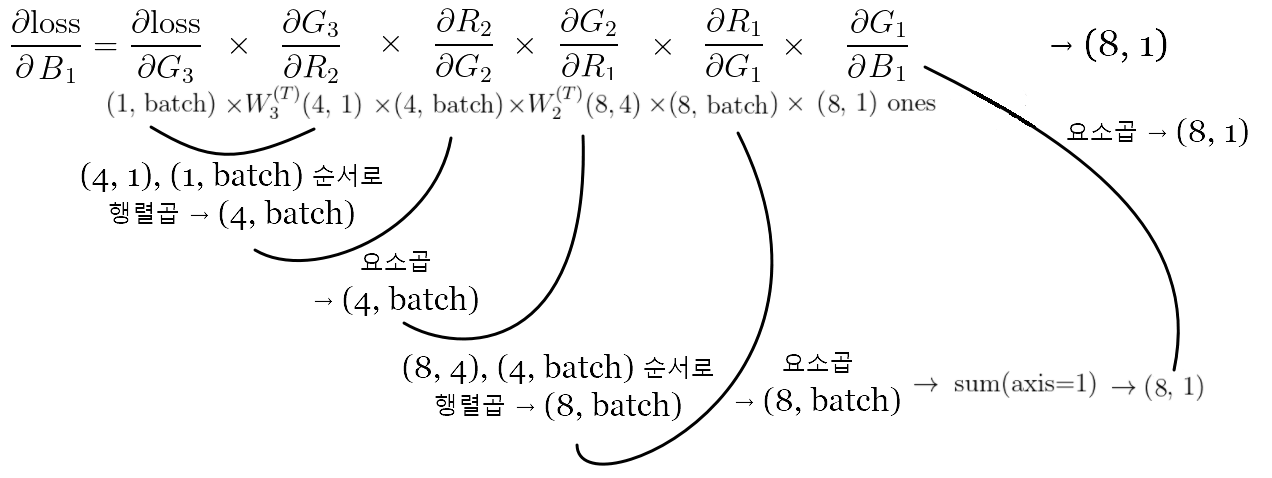
와 길다(...)

 

 

 

4. 연산의 의미

아래의 선형 연산의 결과와 가중치 행렬의 shape을 자세히 보자.

 

 

 

 

G1에서 입력은 (1, batch) 였는데 출력은 (8, batch)로 증폭되었다. 

이렇게 입력과 연결하여 연산하고, 출력을 결정하는 단위를 '노드(node)' 라고 한다. 몇 개의 단위로 증폭, 감소가 되는지 쉽게 알 수 있다. 즉, G1에서의 노드는 8, G2에서의 노드는 4, G3에서의 노드는 1이라고 볼 수 있다.

 

 

 

이를 그림으로 표현하면 어디서 본 것 같은 그림이 나온다.

입력과 연산하는 G1을 Input Layer 입력층

중간 G2 연산을 Hidden Layer 은닉층

출력이 되는 G3 연산을 Output Layer 출력층 이라고 한다.

 

데이터 feature의 수가 노드 개수라고 생각하면 쉽다. 

 

 

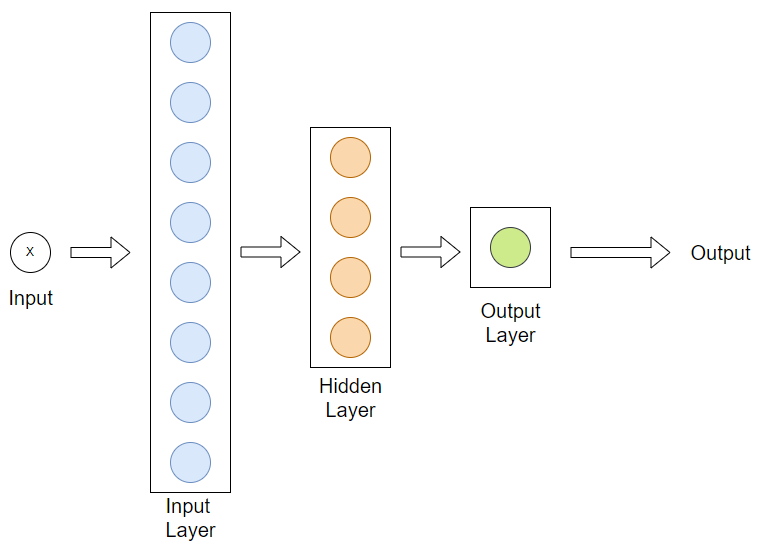
노드 수의 규칙은 있을까? 솔직히 말하면 없다. 딥러닝의 수수께끼 중 하나로 어떤 특정 노드 개수에서 학습이 잘 된다는 것인데 많은 수록 좋은게 아니다. 딥러닝 규칙은 추후에 더 다루겠다.

 

다음 시간에 이를 Numpy 코드로 표현하고 Pytorch와 비교해 보겠다.