경사하강법(Gradient descent)은 오차함수의 기울기를 구하고 기울기의 절대값이 낮은 쪽으로 계속 이동시켜 오차를 최소화하는 방법이다.
지금까지 사용한 경사하강법 방법은 아래와 같이 오차함수의 기울기를 구하고 Weight값과 Bias 값을 수정하였다.
for i in range(Epochs):
dL_dW1, dL_dB1, dL_dW2, dL_dB2, dL_dW3, dL_dB3 = loss_gradient(inputs, targets, W1, B1, W2, B2, W3, B3)
W1 = W1 + -1*learning_rate * dL_dW1
B1 = B1 + -1*learning_rate * dL_dB1
W2 = W2 + -1*learning_rate * dL_dW2
B2 = B2 + -1*learning_rate * dL_dB2
W3 = W3 + -1*learning_rate * dL_dW3
B3 = B3 + -1*learning_rate * dL_dB3
가장 간단하지만 그 만큼 여러 가지 문제점을 가지고 있어 최소화하는데 여러 문제점을 일으킨다.
1. 발산 가능성
예를 들어 아래와 같이 loss(x) = x^(2) 형태의 오차함수가 있다고 가정하자.

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
fig = plt.figure()
ax = plt.axes(xlim=(-10, 10))
def loss_function(x):
return x**2
xrange = np.arange(-10, 10, 0.2)
loss_array = []
for x in xrange:
loss = loss_function(x)
loss_array.append(loss)
ax.plot(xrange, loss_array)
ax.set_xlabel('x')
ax.set_ylabel('loss')
plt.show()
x = -4 위치에서 시작하고 learning rate = 1.05 라고 설정해 보자.
경사하강법 업데이트 규칙에 따라 x = x + -learning_rate*dloss/dx 로 수정해야 한다.
x^(2)의 도함수는 2x이다. 직접 손으로 계산해 보면
x = -4 + -1.05*2*(-4) = 4.4
최소값은 x = 0 이므로 다음 업데이트 위치는 -4 < x < 4 이여야 하는데 벗어나 버린다! 계속 이상태로 업데이트 한다면 x의 위치는 계속 바깥쪽으로 갈테고 결국에는 발산해 버린다. 아래는 과정을 나타낸 코드와 동영상을 첨부한다. 구현방법은 FuncAnimation을 이용하여 실시간 그래프 그리기 편을 참고하길 바란다.
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
import matplotlib.animation as animation
fig = plt.figure()
ax = plt.axes(xlim=(-10, 10))
start_x = -4
learning_rate = 1.05
def loss_function(x):
return x**2
def loss_gradient(x):
return 2*x
xrange = np.arange(-10, 10, 0.2)
loss_array = []
for x in xrange:
loss = loss_function(x)
loss_array.append(loss)
ax.plot(xrange, loss_array)
ax.set_xlabel('x')
ax.set_ylabel('loss')
train_x = []
for i in range(20):
dL_dx = loss_gradient(start_x)
start_x = start_x + -1*learning_rate*dL_dx
train_x.append(start_x)
redDot, = ax.plot([], [], 'ro')
def animate(frame):
loss = loss_function(frame)
redDot.set_data(frame, loss)
return redDot
ani = FuncAnimation(fig, animate, frames=train_x)
#FFwriter = animation.FFMpegWriter(fps=1)
#ani.save('animation.mp4', writer = FFwriter)
plt.show()
2. 수렴까지 너무 느리다.
위의 코드에서 learning rate = 0.001로 수정해 보자. 어떤 일이 일어날까?
3. 지역 최소지점에 빠질 가능성
learing rate를 작게 설정하면 시간은 오래 걸린지언정 언젠가 수렴할 것 같다. 그러나 learning rate를 너무 작게 설정하면 지역 최소지점(Local minimum)에 빠질 가능성이 높다. 이게 무슨 얘기인지 그림을 보면서 이해해 보도록 하자.
예를 들어 오차함수가 아래와 같다고 가정하자.

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
fig = plt.figure()
ax = plt.axes(xlim=(-10, 10))
def loss_function(x):
return (1/200)*(x-9)*(x-1)*(x+1)*(x+6) + 4
xrange = np.arange(-10, 10, 0.2)
loss_array = []
for x in xrange:
loss = loss_function(x)
loss_array.append(loss)
ax.plot(xrange, loss_array)
ax.set_xlabel('x')
ax.set_ylabel('loss')
plt.show()

그래프에서 왼쪽이 국소 최소점(Local minimum)이고 오른쪽이 전체 최소점(Global minimum)이다. 우리의 목표는 가중치 역할을 하는 x가 전체 최소점으로 수렴하게 만들어야 한다.
위 함수를 미분하면 아래와 같다.

1) 시작 위치가 다른 경우
시작위치가 어디인가에 따라 국소 최소점에 수렴할 수도, 전체 최소점에 수렴할수도 있다. learning rate = 1로 고정시켰다. 아래는 확인해 볼 수 있는 코드이다. start_x를 변경하면서 여러 경우를 녹화하였다.
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
import matplotlib.animation as animation
fig = plt.figure()
ax = plt.axes(xlim=(-10, 10))
start_x = -6
learning_rate=1
def loss_function(x):
return (1/200)*(x-9)*(x)*(x+1)*(x+6) + 4
def loss_gradient(x):
return (1/100)*(2*np.power(x, 3)-3*np.power(x, 2)-57*x-27)
xrange = np.arange(-10, 10, 0.1)
loss_array = []
for x in xrange:
loss = loss_function(x)
loss_array.append(loss)
ax.plot(xrange, loss_array)
ax.set_xlabel('x')
ax.set_ylabel('loss')
train_x = []
for i in range(50):
if i == 0:
pass # 첫 위치를 train_x 배열에 입력하기 위해 분기 설정
else:
dL_dx = loss_gradient(start_x)
start_x = start_x + -1*learning_rate*dL_dx
train_x.append(start_x)
redDot, = ax.plot([], [], 'ro')
def animate(frame):
loss = loss_function(frame)
redDot.set_data(frame, loss)
return redDot
ani = FuncAnimation(fig, animate, frames=train_x)
#FFwriter = animation.FFMpegWriter(fps=5)
#ani.save('sx-6lr1.mp4', writer = FFwriter)
plt.show()
(1) start_x = -6, learning rate = 1일 때 국소 최소점에 수렴함.
(2) start_x = -8, learning rate = 1일 때 국소 최소점을 지나쳐 전체 최소점에 수렴함.
(3) start_x = 10, learning rate = 1일 때 전체 최소점을 지나쳐 국소 최소점에 수렴함.
(4) start_x = 7, learning rate = 1일 때 국소 최소점에 수렴함.
왜 이런일이 발생하냐면 시작 위치에서의 기울기가 저마다 다르기 때문이다. start_x가 -8일 때와 -6일 때 직접 손으로 계산해 보도록 하겠다.
start_x = -8일 때

start_x = -6일 때

그래표에 점을 표현하면 아래와 같다.
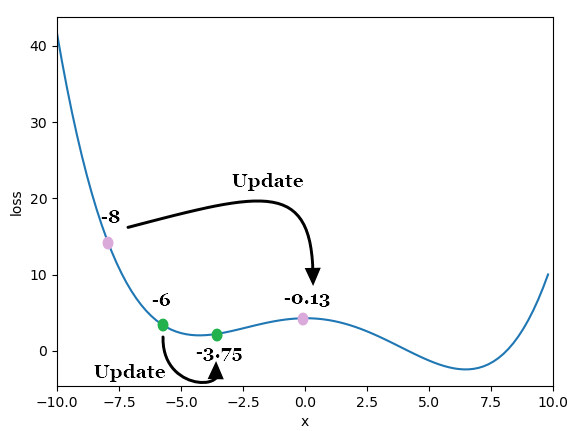
start_x = -8일때의 기울기가 start_x = -6 일 때 보다 크다! (그래프에서 기울기 정도를 직접 확인해 보자.) 그러면 경사하강법 식에 따라 기울기가 곱해지므로 다음 위치는 보다 멀리 가게 되는 것이다. 그래서 -8일 때 지역 최소점을 지나칠 수 있는 것이다. -6일 때 곱해진 기울기가 작으므로 다음 위치가 멀리가지 못하는 것이고 지역 최소점에 같히게 된다.
start_x가 10일 때와 7일 때 원리는 같다. 직접 손으로 계산해 보자.
2) 학습률이 다른 경우
start_x = -8 일 때 learning rate= 1이면 지역 최소점에 같히지 않았는데 0.5이면 아래와 같이 같히게 된다.
기존 경사하강법의 문제점을 요약 정리하자면 아래와 같다.
1. 학습률이 크면 발산할 수 있다.
2. 학습률이 너무 작으면 시간이 오래 걸린다.
3. 학습률이 작으면 수렴은 가능하나 지역 최소점에 같힐 수 있다.
1) 위치에 따라 지역 최소점 또는 전체 최소점에 수렴하는 정도가 달라진다.
2) 학습률에 따라 지역 최소점 또는 전체 최소점에 수렴하는 정도가 달라진다.
다음 시간에는 이를 어떻게 개선할 수 있는지 이야기해 볼 것이다.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 21. 경사하강법의 개선 - Adam (0) | 2022.02.05 |
|---|---|
| 20. 경사하강법의 개선 - Momentum, RMSprop (0) | 2022.02.04 |
| 18. 다층 퍼셉트론(MPL)의 등장-2.비선형 회귀식(실습) (0) | 2022.01.21 |
| 17. 다층 퍼셉트론(MPL)의 등장-2.비선형 회귀식(심화이론) (0) | 2022.01.21 |
| 16. 다층 퍼셉트론(MPL)의 등장-2.비선형 회귀식(기초이론) (0) | 2022.01.20 |



