이전 시간까지 1개 채널을 가진 이미지를 1개의 필터를 이용하여 특성을 추출한 후 학습을 진행하였다. 1개 채널을 가진 이미지로 만들기 위해 흑백이미지(Grayscale)로 만들어 학습시켰다.
하지만, 색깔도 엄연히 이미지의 특징에 해당된다. 예를 들어 아래 사진의 색맹분들 처럼 입력 데이터에 색깔 정보가 없다면, 인공신경망은 잘못된 학습을 할 가능성이 높다.

색상에 대한 정보를 어떻게 다루어야 하는지 CNN 시리즈 마지막 포스트로 이야기 하고자 한다.
1. 채널(channel)
채널이란 영상 또는 이미지의 색상에 대한 정보를 담은 객체라고 생각해 볼 수 있으며 일반적으로 아래와 같이 R, G, B, Alpha로 구성되어 있다.

아래 코드를 통해 직접 확인해 보자.
import numpy as np
import cv2
import matplotlib.pyplot as plt
from google.colab.patches import cv2_imshow
image_path = '여러분의 경로'
image = cv2.imread(image_path)
b, g, r = cv2.split(image)
add_img = cv2.hconcat([b, g, r])
cv2_imshow(image)
cv2_imshow(add_img)
순서대로 Original, B, G, R인데 색상정보가 없이 흑백으로 출력된다. 그 이유는 1개 채널이라 GrayScale로 인식하기 때문이다. 이를 우리가 생각하는 색상을 표현하기 위해(셀로판지로 바라본 사진이라고 생각해도 된다.) 다른 채널 정보를 0으로 입력하면 된다.
# 사람 눈에 익숙한 이미지로 보이도록 다른 채널을 0으로 만들어서 합치면 됨.
# 이렇게 하면 색상 채널이 있는 정보가 강조되어 출력됨.
zeros = np.zeros((image.shape[0], image.shape[1]), dtype="uint8")
img_b = cv2.merge([b, zeros, zeros])
img_g = cv2.merge([zeros, g, zeros])
img_r = cv2.merge([zeros, zeros, r])
add_img = cv2.hconcat([img_b, img_g, img_r])
cv2_imshow(add_img)

이제야 우리가 아는 이미지 형태가 출력되었다.
2. 다채널 이미지에 대한 합성곱
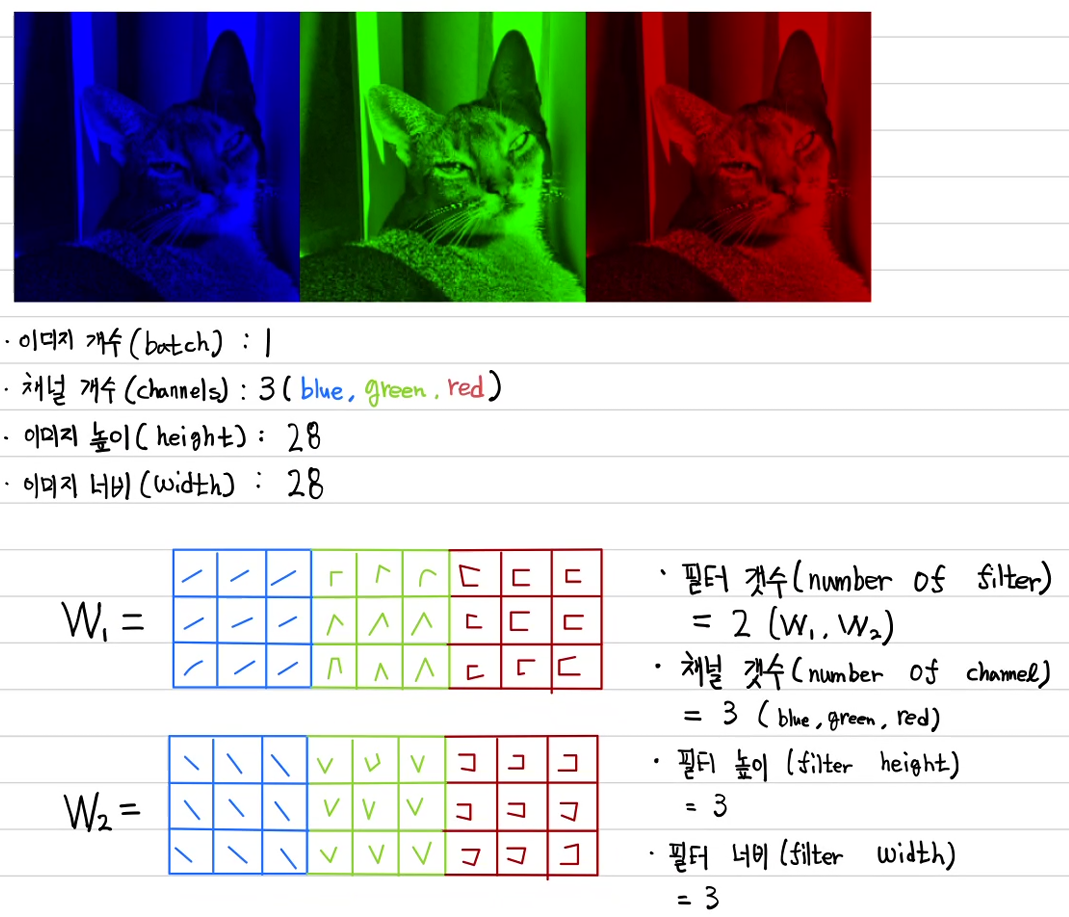
위와 같은 3채널을 갖는 이미지를 1개의 3 × 3 필터로 합성곱을 할 때 필터는 어떤 shape을 갖고 있을까? 앞의 예제에서 흑백 이미지에 대해 1개의 3 × 3 필터를 사용하였다. 흑백 이미지는 1개의 채널이므로 이때의 필터 shape은 (1, 3, 3)이다.
따라서 3채널을 갖는 이미지를 1개의 3 × 3 필터로 합성곱을 한다면 필터의 shape은 (3, 3, 3)이 되어야 한다.
조금 더 확장해서 이미지가 (batch, channel, height, width)으로 구성되어 있다면 합성곱 필터는 (number of filter, number of channel, height, width)로 구성되어야 한다.
예를 들어 위의 고양이 사진 1개에 대한 이미지 형식은 (1, 3, 28, 28)이고 만약 이를 2개의 3×3 합성곱 필터를 사용한다고 하면 합성곱 필터의 shape은 (2, 3, 3, 3)이 되는 것이다.
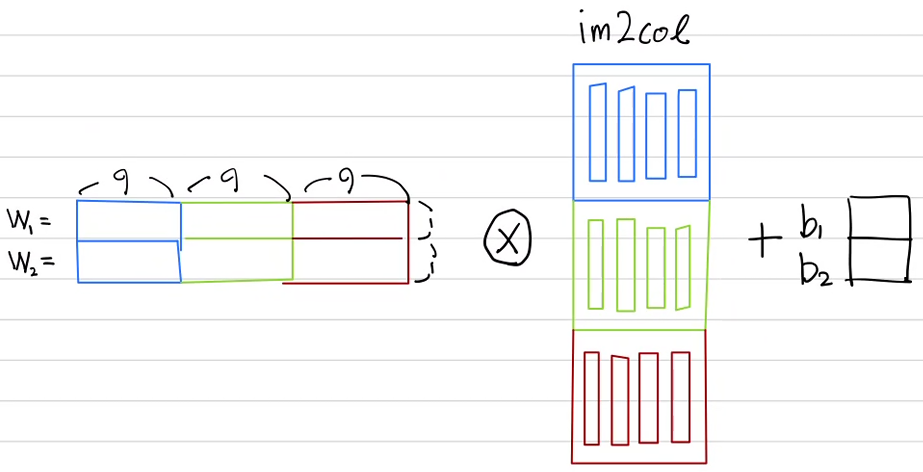
위 상황을 im2col을 이용하여 합성곱을 하려면 어떻게 처리해야 할까? 이미지는 im2col을 실시하여 아래로 이어 붙인다. 여러개의 필터가 있을 땐 먼저 필터를 1차원으로 쭉 펴서 가로로 이어 붙이고 다른 필터는 아래로 이어 붙인 후 합성곱을 하면 된다. 위의 말을 그림으로 표현하면 아래와 같다.
이를 코드로 어떻게 구현해야 할까? 아쉽지만 본인이 짠 코드는 과정을 이해하기 위해 조금 번거롭게 작성한 코드여서 다채널 합성곱에선 정말정말 비효율적이다. 따라서 이번 포스트에서는 개념만 잡고 따로 구현하지 않겠다. 작성 방법이 궁금하다면 딥러닝 공부의 영원한 베스트 셀러 '밑바닥부터 시작하는 딥러닝 1권'의 7장 합성곱 파트를 보면 된다.
그래도 하나라도 구현 안하면 서운하니, '33. [CNN기초] 이미지의 합성곱 훈련 -쉬운예제(실습)-' 에서 훈련이 잘 안된 상황을 보강하는 방법으로 다채널을 사용한 예제를 소개하겠다.
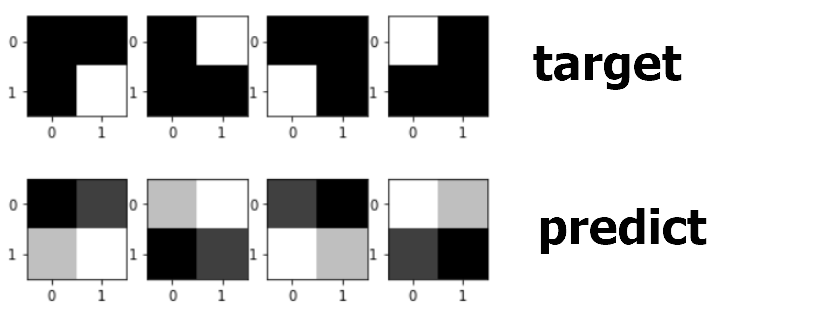
위 예제에서 훈련이 잘 안된 이유를 필터 개수의 부족, 부호화 분류기(fully connected layer) 부재 등으로 뽑았었는데 이를 해결하기 위해 필터 2개를 적용하고 분류기(fc layer)를 도입하여 문제를 해결해 보자.
과정은 아래와 같다. 자세한 코드 내용은 '35. [CNN기초] 원, 네모를 구별하는 CNN 만들기(이론)' 과 '36. [CNN기초] 원, 네모를 구별하는 CNN 만들기(실습)' 과 동일하니 비교하면서 보길 바란다.

주목할 점은 numpy dot이 아닌 numpy matmul 메서드를 사용한 것이다. 이 함수는 3차원 배열 행렬곱에 매우 유용한데 예를 들어 W = (a, b)이고 X = (batch, b, c) 일 때 matmul 메서드는 batch 단위로 계산하여 리턴해 준다. 즉 matmul(W, X) = (batch, a, c)이다. 이를 이용하면 for문을 사용하지 않아도 된다.
그 외 과정은 '33. [CNN기초] 이미지의 합성곱 훈련 -쉬운예제(실습)-' 과 거의 유사하다. 전체적인 코드를 보자.
import numpy as np
import matplotlib.pyplot as plt
x_sorce1 = np.array([[0.1, 0.2, 0.3],
[0.4, 0.5, 0.6],
[0.7, 0.8, 0.9]])
x_sorce2 = np.flipud(x_sorce1) # sorce1의 좌우반전
x_sorce3 = np.fliplr(x_sorce1) # sorce1의 상하반전
x_sorce4 = np.fliplr(x_sorce2) # sorce2의 좌우반전
X = np.stack((x_sorce1, x_sorce2, x_sorce3, x_sorce4))
y_sorce1 = np.array([[0., 0.],
[0., 1.]])
y_sorce2 = np.flipud(y_sorce1) # sorce1의 좌우반전
y_sorce3 = np.fliplr(y_sorce1) # sorce1의 상하반전
y_sorce4 = np.fliplr(y_sorce2) # sorce2의 좌우반전
Y = np.stack((y_sorce1, y_sorce2, y_sorce3, y_sorce4))
fig, ax = plt.subplots(2, 4)
for x in range(4):
ax[0][x].imshow(X[x], cmap='gray')
for y in range(4):
ax[1][y].imshow(Y[y], cmap='gray')
plt.show()
np.random.seed(230207)
Wc = np.random.randn(2, 2, 2)
Bc = np.random.randn(2, 1)
Wf = np.random.randn(4, 8)
Bf = np.random.randn(4, 1)
conv_stride = 1
conv_padding = 0
conv_filter_size = 2
out_conv_size = 2 # (3 - 2 + 1*0)/1 + 1
def im2col(input, stride, padding, filter_size, output_size):
count = 0
input = np.pad(input, ((padding, padding), (padding, padding)))
for o_h in range(output_size):
for o_w in range(output_size):
a = input[stride*o_h : stride*o_h + filter_size, stride*o_w:stride*o_w + filter_size]
out = np.reshape(a, (1, -1))
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out), axis=0)
count += 1
return np.transpose(outs, (1, 0))
def Conv2D(inputs, stride, padding, filter_size, output_size, weight, bias):
count = 0
for input in X:
img_to_col = im2col(input=input, stride=conv_stride, padding=conv_padding,
filter_size=conv_filter_size, output_size=out_conv_size)
img_to_col = img_to_col[np.newaxis, :, :]
if count == 0:
outs = img_to_col.copy()
else:
outs = np.concatenate((outs, img_to_col))
count += 1
W = np.reshape(weight, (weight.shape[0], -1))
convs = np.matmul(W, outs) + bias
convs = np.reshape(convs, (-1, weight.shape[0], output_size, output_size))
return convs
def fc_layer(input):
return np.dot(Wf, np.transpose(input, (1, 0))) + Bf
def sigmoid(input):
return 1 / (1 + np.exp(-input))
def loss_func(pred, target):
return np.sum(-target*np.log(pred) - (1-target)*np.log(1-pred))
def forward(inputs, target):
conv = Conv2D(inputs=X, stride=conv_stride, padding=conv_padding,
filter_size=conv_filter_size, output_size=out_conv_size,
weight=Wc, bias=Bc)
# (batch, 2, 2, 2)
flatten = conv.reshape((conv.shape[0], -1)) # (batch, 8)
fc = fc_layer(flatten) # (4, batch)
pred = sigmoid(fc) # (4, batch)
# 오차 구하기, Y값 (batch, 2, 2)를 예측값(4, batch)에 맞게 reshape()
# (batch, 2, 2) -> reshape (batch, 4) -> transpose (4, batch)
target = target.reshape(-1, pred.shape[0]) #(batch, 2, 2) -> (batch 4)
target_T = np.transpose(target, (1, 0)) # (batch, 4) -> (4, batch)
losses = loss_func(pred, target_T)
return losses, pred, fc, flatten, conv
def loss_gradient(inputs, targets):
# 순전파 실행, 순서대로 scalar, (4, batch), (4, batch), (batch, 8), (batch, 2, 2, 2)
_, pred, fc, flatten, convs = forward(inputs, targets)
Y = np.transpose(targets.reshape(-1, pred.shape[0]), (1, 0)) # (batch, 2, 2) -> (batch, 4) -> (4, batch)
dL_dsig = -1*( (Y / pred) - ( (1-Y) / (1-pred) ) ) # (4, batch)
#print(dL_dsig)
dsig_dfc = ( 1/(1+np.exp(-fc)) ) * ( 1 - 1/(1+np.exp(-fc)) ) # (4, batch)
#print(dsig_dfc)
dL_dfc = dL_dsig * dsig_dfc # (4, batch)
#print(dL_dfc)
dfc_dWf = flatten #(batch, 8)
#print(flt)
# Wl과 Bl을 구해봅시다.
dL_dWf = np.dot(dL_dfc, dfc_dWf) # (4, batch) × (batch, 8) = (4, 8)
#print(dL_dWf)
dL_dBf = np.sum(dL_dfc, keepdims=True, axis=1) # (4, 1)
#print(dL_dBf)
dfc_dflatten = np.transpose(Wf, (1, 0)) # (8, 4)
#print(dfc_dflat)
dL_dflatten = np.dot(dfc_dflatten, dL_dfc) # (8, 4) × (4, batch) = (8, batch)
#print(dL_dflat)
#flaten은 형변환이므로 출력인 dL_dflaten을 conv 출력 연산 shape으로 바꾸어주어야 한다.
# (8, batch) -> (batch, 8) -> (batch, 2, 4)
dflatten_dconv = np.transpose(dL_dflatten, (1, 0)) #(8, batch) -> (batch, 8)
dL_dconv_s = np.reshape(dflatten_dconv, (-1, 2, 4)) # batch, 8) -> (batch, 2, 4)
#Wc, Bc 구하기
"""input의 im2col의 전치"""
count = 0
for input in inputs:
img_to_col = im2col(input=input, stride=conv_stride, padding=conv_padding,
filter_size=conv_filter_size, output_size=out_conv_size)
img_to_col = img_to_col[np.newaxis, :, :]
if count == 0:
outs = img_to_col.copy()
else:
outs = np.concatenate((outs, img_to_col))
count += 1
dconv_dWc_s = np.transpose(outs, (0, 2, 1)) # (batch, 4, 4)
"""batch 단위의 행렬곱 실시하여 dL_dWc 계산 """
dL_dWc_sum = 0
for dL_dconv, dconv_dWc in zip(dL_dconv_s, dconv_dWc_s):
dL_dWc = np.dot(dL_dconv, dconv_dWc)
dL_dWc_sum += dL_dWc # (2, 4)
dL_dWc = np.reshape(dL_dWc_sum, Wc.shape) # (2, 2, 2)
dL_dBc = np.sum(dL_dconv_s, keepdims=True, axis=2) # (batch, 2, 4) -> (batch, 2, 1)
dL_dBc = np.sum(dL_dBc, axis=0) # (batch, 2, 1) -> (2, 1)
return dL_dWf, dL_dBf, dL_dWc, dL_dBc
_, predict, _, _, _ = forward(X, Y)
predict = np.reshape(predict, Y.shape)
for pred in range(4):
plt.subplot(1, 4, pred+1)
plt.imshow(predict[pred], cmap='gray')
plt.show()
# 경사하강법 적용
learning_rate = 0.01
epochs = 1000
for epoch in range(epochs+1):
loss, pred, _, _, _, = forward(X, Y)
dL_dWf, dL_dBf, dL_dWc, dL_dBc = loss_gradient(X, Y)
Wf = Wf + -1*learning_rate*dL_dWf
Bf = Bf + -1*learning_rate*dL_dBf
Wc = Wc + -1*learning_rate*dL_dWc
Bc = Bc + -1*learning_rate*dL_dBc
if epoch % 100 == 0:
print('epoch :', epoch, '\n', 'loss :', loss, '\n', 'forward :' , '\n', pred)
fig2, ax2 = plt.subplots(2, 4)
_, predict, _, _, _ = forward(X, Y)
predict = np.reshape(predict, Y.shape)
for y in range(4):
ax2[0][y].imshow(Y[y], cmap='gray')
for pred in range(4):
ax2[1][pred].imshow(predict[pred], cmap='gray')
plt.show()
결과를 확인해 보자
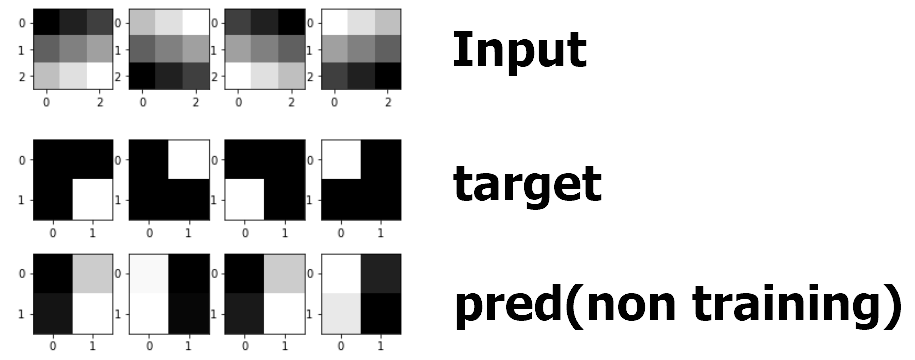
input에 대하여 pred는 아직 훈련되지 않았다. 이를 target에 맞게 훈련시켜 보자.
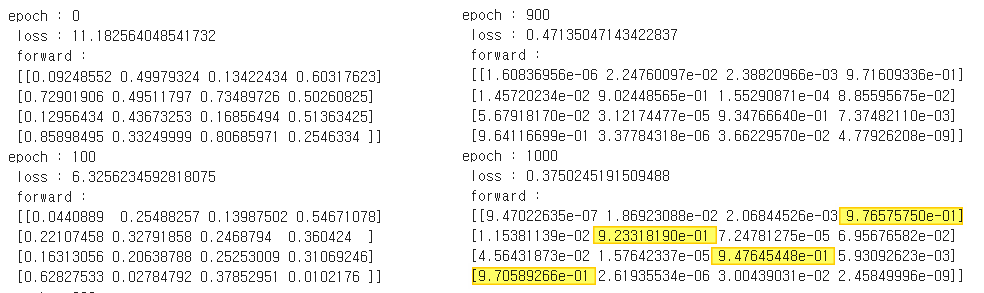
1000회 훈련시켰더니 잘 된다. 결과를 확인해 보자.

훈련이 매우 잘 되었다.
이것으로 CNN의 기초를 마치고자 한다. RNN을 하려고 하는데... 요새 핫한 GPT-3도 sqs2sqs의 attention을 응용한 방식이므로 RNN, LSTM, GRU를 반드시 해야 하는데 이건 numpy로 작성하기가 더 어렵다...
그리고 결론적으로 본인이 개학을 하기 때문에 다시 본업인 물리수업을 준비해야 한다 (ㅜㅜ)
여름방학이 될지 아니면 이번처럼 다시 겨울방학에 할 수 있을지 장담할 수 없지만... 올 한해 시계열 데이터를 열심히 공부하여 RNN에 대한 Numpy 포스팅을 다음에 시작하겠다! 모두 건강하시길...
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 39.[RNN기초] RNN(many to one) 순전파 구현(이론) (0) | 2023.09.12 |
|---|---|
| 38.[RNN기초] 자연어 데이터는 어떻게 접근해야 할까? (0) | 2023.09.11 |
| 36. [CNN기초] 원, 네모를 구별하는 CNN 만들기(실습) (2) | 2023.02.01 |
| 35. [CNN기초] 원, 네모를 구별하는 CNN 만들기(이론) (2) | 2023.01.28 |
| 34. [CNN기초] Max pooling, Average pooling 구현 (0) | 2023.01.26 |



