저번시간에 'hello'라는 단어를 이용하여 아래와 같이 순서대로 출력하는 many to many RNN 신경망을 어떻게 순전파 할 수 있는지 탐구하였다.
1. h 입력 → e 출력
2. e 입력 → l 출력
3. l 입력 → l 출력
4. l 입력 → o 출력

이 때 hyper parameters는 아래와 같이 설정하였다.
1. many to many 역전파
조금만 생각하면 역전파는 어렵지 않다. 아래와 같이 분할해서 생각해 보면 many to one 역전파를 time step 역순으로 여러 번 실시하는 것과 같다.

위의 그림에 따라, 역전파 순서를 글로 표현하면 다음과 같아야 한다.
<time step = 3 에서 역전파 실시>
3 번째 fc 분류기 역전파 실시
이전 상태인 fc분류기 기울기를 받고 현재 t= 3 rnn셀 역전파 실시
이전 상태인 rnn셀의 기울기를 받고 현재 t= 2 rnn셀 역전파 실시
이전 상태인 rnn셀의 기울기를 받고 현재 t= 1 rnn셀 역전파 실시
이전 상태인 rnn셀의 기울기를 받고 현재 t= 0 rnn셀 역전파 실시
<time step = 2 에서 역전파 실시>
2 번째 fc 분류기 역전파 실시
이전 상태인 fc분류기 기울기를 받고 현재 t= 2 rnn셀 역전파 실시
이전 상태인 rnn셀의 기울기를 받고 현재 t= 1 rnn셀 역전파 실시
이전 상태인 rnn셀의 기울기를 받고 현재 t= 0 rnn셀 역전파 실시
<time step = 1 에서 역전파 실시>
1 번째 fc 분류기 역전파 실시
이전 상태인 fc분류기 기울기를 받고 현재 t= 1 rnn셀 역전파 실시
이전 상태인 rnn셀의 기울기를 받고 현재 t= 0 rnn셀 역전파 실시
<time step = 0 에서 역전파 실시>
0 번째 fc 분류기 역전파 실시
이전 상태인 fc분류기 기울기를 받고 현재 t= 0 rnn셀 역전파 실시
위를 다중 for문으로 표현하면 아래와 같다.
for t_s in reversed(range(time_steps)):
print(" ")
print("<time step = ", t_s, "에서 역전파 실시>")
print(t_s,"번째 fc 분류기 역전파 실시")
for t in reversed(range(t_s+1)) :
if t == t_s:
print("이전 상태인 fc분류기 기울기를 받고 현재 t=",t, "rnn셀 역전파 실시")
else:
print("이전 상태인 rnn셀의 기울기를 받고 현재 t=",t, "rnn셀 역전파 실시")many to one과 다른 점은, fc 분류기도 for문으로 순회를 돈다는 것이다. 그외의 코드는 거의 같다.
아래는 역전파 코드이다 many to one과 차이점은 다음과 같다.
- Wy, By의 기울기를 누적할 변수(list) 추가
- 첫 번째 for문 for t_s in reversed(range(time_steps)): 에서는 fc 분류기에 대한 역전파를 실시
fc 분류기 역전파 실시 후 기울기 변수에 추가 - 두 번째 for문 for t in reversed(range(t_s+1)): 에서는 rnn 셀에 대한 역전파를 실시
rnn 셀 역전파 실시 후 기울기 변수에 추가
def loss_gradient(X, Y):
dE_dWxh_list = np.zeros_like(Wxh) # (s.l(4), h.n(3)) 기울기 누적 변수
dE_dWhh_list = np.zeros_like(Whh) # (h.n(3), h.n(3)) 기울기 누적 변수
dE_dBh_list = np.zeros_like(Bh) # (1, 1) 기울기 누적 변수
dE_dWy_list = np.zeros_like(Wy) # (h.n(3), o.f(4)) 기울기 누적 변수
dE_dBy_list = np.zeros_like(By) # (1, 1) 기울기 누적 변수
#순전파
predics, pred_list, pred_i_list, ht_list, ht_i_list = rnn_cell(X)
# hi_i_list는 [h0_i, h1_i, h2_i, h3_i] 순서
# ht_list는 [h-1, h0, h1, h2, h3] 순서
loss = CEE_loss(predics, Y)
count = 0
for t_s in reversed(range(time_steps)):
# 역전파 실시
dE_dpred_i = pred_list[t_s] - Y[t_s]
#fc 분류기에 대한 기울기 구하기 실시
dpred_i_dWy = np.transpose(ht_list[t_s+1], (1, 0))
dE_dWy = np.dot(dpred_i_dWy, dE_dpred_i)
dE_dBy = np.sum(dE_dpred_i, keepdims=True)
dE_dWy_list += dE_dWy
dE_dBy_list += dE_dBy
for i in reversed(range(t_s+1)) :
if i == t_s:
dht_plus1_i_dht = np.transpose(Wy, (1, 0))
dE_dth_plus1_i = dE_dpred_i
else:
dht_plus1_i_dht = np.transpose(Whh, (1, 0))
dE_dth_plus1_i = dE_dht_i
dE_dht = np.dot(dE_dth_plus1_i, dht_plus1_i_dht)
dht_dht_i = (1-np.power(np.tanh(ht_i_list[i]), 2))
dE_dht_i = dE_dht * dht_dht_i
# dE_dWxh 구하기
dht_i_dWxh = np.transpose(np.reshape(X[i], (1, -1)), (1, 0))
# X를 그냥 가지고 오면 1차원 배열이여서 2차원으로 바꾸어주어야 함
dE_dWxh = np.dot(dht_i_dWxh, dE_dht_i)
# dE_dWhh 구하기
dht_i_dWhh = np.transpose(ht_list[i], (1, 0))
dE_dWhh = np.dot(dht_i_dWhh, dE_dht_i)
# dE_dBh 구하기
dE_dBh = np.sum(dE_dht_i, keepdims=True)
# 기울기 누적
dE_dWxh_list += dE_dWxh
dE_dWhh_list += dE_dWhh
dE_dBh_list += dE_dBh
return dE_dWy_list, dE_dBy_list, dE_dWxh_list, dE_dWhh_list, dE_dBh_list
print(loss_gradient(input_RNN[0], targets[0]))
잘 될까? 아래 경사하강법으로 훈련하고 결과를 확인해 보자
# 훈련 전 예측값
pred, _, _, _, _ = rnn_cell(input_RNN[0])
print('before pred', pred)
learning_rate = 0.005
for i in range(2000):
dL_dWy, dL_dBy, dL_dWxh, dL_dWhh, dL_dBh = loss_gradient(input_RNN[0], target[0])
Wy = Wy + -1*learning_rate * dL_dWy
By = By + -1*learning_rate * dL_dBy
Wxh = Wxh + -1*learning_rate * dL_dWxh
Whh = Whh + -1*learning_rate * dL_dWhh
Bh = Bh + -1*learning_rate * dL_dBh
if i % 100 == 0:
pred, _, _, _, _ = rnn_cell(input_RNN[0])
print(i, CEE_loss(pred, targets[0]))출력결과
before pred
[ [0.06397614 0.03819114 0.85299781 0.0448349 ]
[0.0403228 0.76902459 0.06926133 0.12139129]
[0.27148641 0.47031804 0.03033868 0.22785687]
[0.19165547 0.02808298 0.7083062 0.07195535] ]
0 11.995305385065343
100 8.542236164743558
200 7.253592358973341
300 6.544396677982483
400 5.995739152192827
500 5.742292420310077
600 5.6522130480782815
700 5.612021495038995
800 5.58417699010521
900 5.565104086398525
1000 5.5549817621692865
1100 5.5502348707000575
1200 5.547996947460872
1300 5.546874182259792
1400 5.546265877072143
1500 5.545911904998333
1600 5.545693327490806
1700 5.545551769519191
1800 5.545456506378257
1900 5.545390345216081
# 훈련 후 예측값
pred, _, _, _, _ = rnn_cell(input_RNN[0])
print('after pred', pred)출력 결과
after pred
[ [0.24983103 0.2500011 0.24998167 0.2501862 ]
[0.24993175 0.24999342 0.24999242 0.25008242]
[0.25008197 0.25001243 0.2500092 0.2498964 ]
[0.25005301 0.24998581 0.25000541 0.24995576] ]
2. RNN 역전파 문제점과 Truncated
결과를 보면 전부 0.25다. 직관력을 사용하여 왜 이렇게 된 건지 설명할 수 있다.
softmax 공식을 생각할 때 softmax를 통과하는 모든 값이 0이라면, 1/4이 출력된다.
a = np.array([0, 0, 0, 0])
softmax = np.exp(a) / np.sum(np.exp(a))
print(softmax)출력결과
[0.25 0.25 0.25 0.25]
softmax값을 통과하고자 하는 값들이 0이 되었다는 것인데 아래와 같이 fc 분류기와 rnn 셀 연산을 생각할 때 모두 0이 나오는 경우는 가중치의 값들이 0이 되었다는 것이다!

가중치의 값들이 0이 되었다는 것은 바로 vanishing gradient, 기울기 소실이 발생했다는 것이다.
(16. 다층 퍼셉트론(MPL)의 등장-2.비선형 회귀식(기초이론) (tistory.com) 이 포스팅 참고, sigmoid 함수의 vanishing gradient 문제로 relu를 사용했다는 사실을 다시 한번 기억해 보자)
잘 작동되는 것처럼 보이는 RNN 역전파를 시행할 때 여러가지 문제점이 있다.
- 아래와 같이 tanh의 기울기는 크기가 0보다 크고 1보다 작다. 따라서 tanh 미분값이 역전파 시 계속해서 곱해진다면 기울기가 작아져서 소멸하는 vanishing gradient 문제를 발생시킨다.

- 위의 역전파 과정을 보면 알겠지만 x오차에따른 rnn셀의 가중치 기울기 계산의 총 횟수를 따지면 time step = 0은 4번, time step = 1은 3번 ... time step = 3은 1번 밖에 시행하지 않는다. 이는 편향의 문제를 발생시킬 수 있다.
- 이러한 복잡적인 문제들로 인해 기울기를 무작정 누적시킨다면 기울기값이 0에 수렴하거나 발산할 수 있다.
이를 해결하기 위해 아래와 같이 경사하강법을 끉어서 적용하는 Truncated 방법(TBPTT)이 있다.

아래와 같이, 경사하강법을 time step별로 실시하고 적용할 것이다.
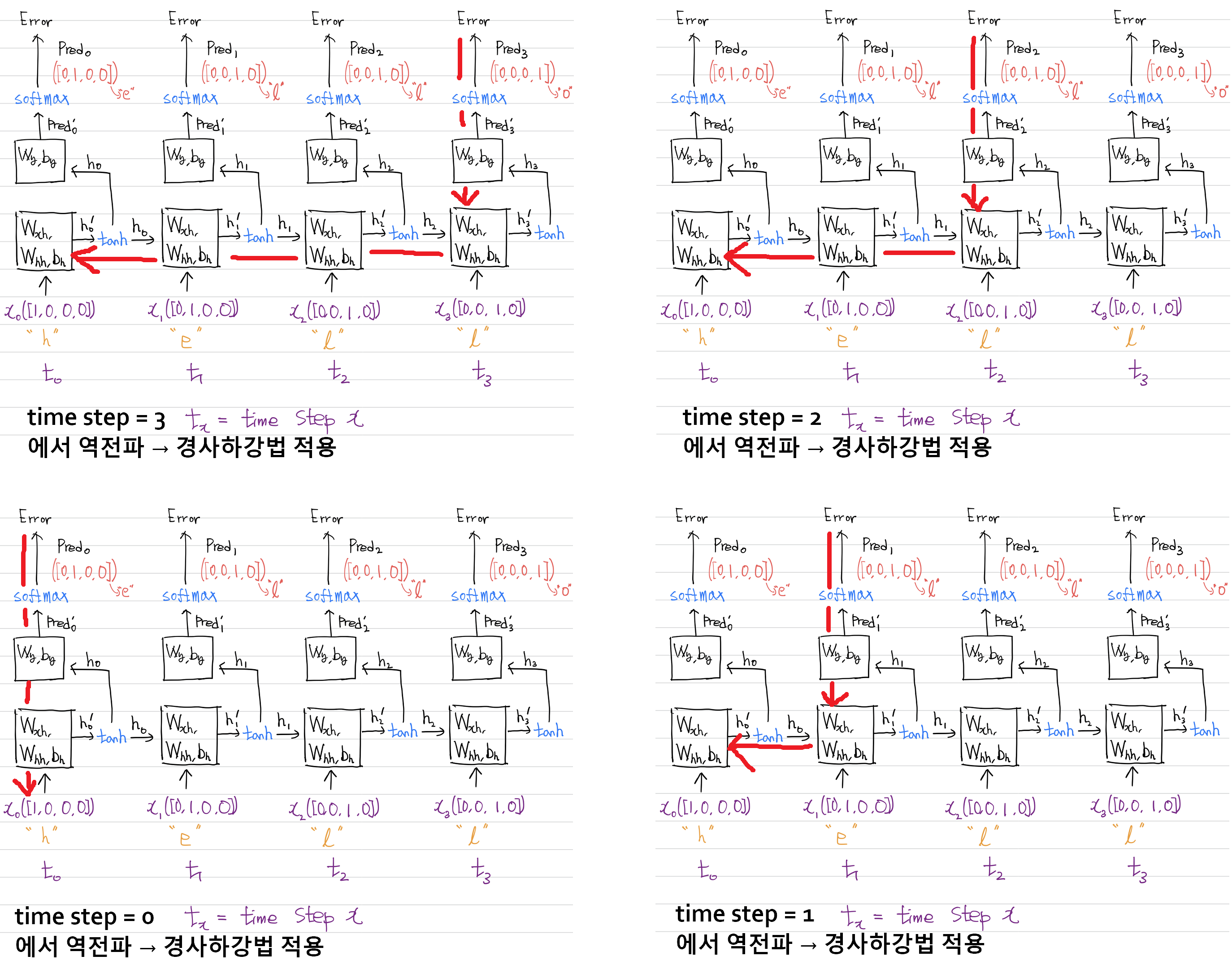
Truncated를 적용한 코드를 살펴보자. loss_gradient 함수에서 바로 경사하강법을 적용할 것이다. 이를 위해 몇 가지 변경점을 살펴보자.
- 경사하강법을 함수 내에서 적용하기 위해, 가중치 변수들을 지역 변수(global)로 선언해야 한다.
- Wy, By를 곧바로 경사하강법을 적용시킬 것이므로 Wy, By에 대한 기울기 누적 함수는 필요 없다.
- time step 단위로 경사강법을 실시한다.
def loss_gradient(X, Y, lr):
global Wy, By, Wxh, Whh, Bh # 전역 변수 선언
dE_dWxh_list = np.zeros_like(Wxh)
dE_dWhh_list = np.zeros_like(Whh)
dE_dBh_list = np.zeros_like(Bh)
# Wy, By 누적 변수 삭제
#순전파
predics, pred_list, pred_i_list, ht_list, ht_i_list = rnn_cell(X)
# hi_i_list는 [h0_i, h1_i, h2_i, h3_i] 순서
# ht_list는 [h-1, h0, h1, h2, h3] 순서
loss = CEE_loss(predics, Y)
count = 0
for t_s in reversed(range(time_steps)):
# 역전파 실시
dE_dpred_i = pred_list[t_s] - Y[t_s]
#fc 분류기에 대한 기울기 구하기 실시
dpred_i_dWy = np.transpose(ht_list[t_s+1], (1, 0))
dE_dWy = np.dot(dpred_i_dWy, dE_dpred_i)
dE_dBy = np.sum(dE_dpred_i, keepdims=True)
for i in reversed(range(t_s+1)) :
if i == t_s:
dht_plus1_i_dht = np.transpose(Wy, (1, 0))
dE_dth_plus1_i = dE_dpred_i
else:
dht_plus1_i_dht = np.transpose(Whh, (1, 0))
dE_dth_plus1_i = dE_dht_i
dE_dht = np.dot(dE_dth_plus1_i, dht_plus1_i_dht)
dht_dht_i = (1-np.power(np.tanh(ht_i_list[i]), 2))
dE_dht_i = dE_dht * dht_dht_i
# dE_dWxh 구하기
dht_i_dWxh = np.transpose(np.reshape(X[i], (1, -1)), (1, 0))
# X를 그냥 가지고 오면 1차원 배열이여서 2차원으로 바꾸어주어야 함
dE_dWxh = np.dot(dht_i_dWxh, dE_dht_i)
# dE_dWhh 구하기
dht_i_dWhh = np.transpose(ht_list[i], (1, 0))
dE_dWhh = np.dot(dht_i_dWhh, dE_dht_i)
# dE_dBh 구하기
dE_dBh = np.sum(dE_dht_i, keepdims=True)
# 기울기 누적
dE_dWxh_list += dE_dWxh
dE_dWhh_list += dE_dWhh
dE_dBh_list += dE_dBh
# time step 단위로 경사하강법 적용
Wy = Wy + -1*lr * dE_dWy
By = By + -1*lr * dE_dBy
Wxh = Wxh + -1*lr * dE_dWxh_list
Whh = Whh + -1*lr * dE_dWhh_list
Bh = Bh + -1*lr * dE_dBh_list
print(loss_gradient(input_RNN[0], targets[0], lr=0.001))
loss_gradient를 여러번 호출하여 경사하강법을 실시한다.
# 훈련 전 예측값
pred, _, _, _, _ = rnn_cell(input_RNN[0])
print('before pred', pred)
for i in range(2000):
loss_gradient(input_RNN[0], targets[0], lr=0.005)
if i % 100 == 0:
pred, _, _, _, _ = rnn_cell(input_RNN[0])
print(i, CEE_loss(pred, targets[0]))출력결과
before pred
[ [0.06421967 0.03826087 0.85256996 0.0449495 ]
[0.04060981 0.76764176 0.07027615 0.12147228]
[0.26839292 0.47363898 0.03059547 0.22737263]
[0.19292056 0.02834739 0.70545919 0.07327286] ]
0 11.79515658524334
100 4.959578421445732
200 3.8864902061821684
300 3.3365350067287416
400 3.0671210403292317
500 2.97612582400557
600 2.9461502059859317
700 2.9154979716596223
800 2.8759475780457127
900 2.840092041101867
1000 2.8161915388443486
1100 2.8019042952954507
1200 2.7896491419146354
1300 2.7656251067003956
1400 2.699229231984696
1500 2.5950109611261034
1600 2.4972545725645796
1700 2.417265166209865
1800 2.3579062697518554
1900 2.316414169055823
# 훈련 후 예측값
pred, _, _, _, _ = rnn_cell(input_RNN[0])
print('after pred', pred)출력 결과
after pred
[ [0.01002641 0.96251158 0.02394973 0.00351228]
[0.04563556 0.35968796 0.36162614 0.23305034]
[0.09699241 0.10147225 0.41357891 0.38795642]
[0.16231759 0.00431234 0.12814991 0.70522016] ]
약 2.3의 오차로 수렴하였고 출력 결과는 깔끔하지 않다. 이건 RNN 셀의 은닉 노드 수가 부족하다는 뜻이다.아래와 같이 hidden node수를 3에서 6으로 늘리고 수행해 보면 아래와 같다.
time_steps = input_RNN.shape[1] # t.s(4)
sequence_length = input_RNN.shape[2] # s.l(4)
hidden_node = 6 # 내가 설정해야 하는 것, 3에서 6으로 증가
output_feature = targets.shape[1] # o.f(4)
출력 결과
before pred
[ [3.24394454e-01 3.89065541e-01 6.23646205e-02 2.24175385e-01]
[1.69186579e-01 2.30567092e-01 3.42921900e-03 5.96817110e-01]
[6.55115321e-03 9.26344723e-01 2.39628192e-04 6.68644959e-02]
[6.20281475e-04 6.23833255e-01 7.67802601e-04 3.74778661e-01] ]
0 15.867816298322511
100 1.7177823033832111
200 1.111257945581254
300 0.8524019952247719
400 0.6141454089919963
500 0.4375735437356167
600 0.35056229976798425
700 0.2952008157918694
800 0.25682387009542507
900 0.22856920030817837
1000 0.20684935044625707
1100 0.1896041743061186
1200 0.17556253753538015
1300 0.16389573067107027
1400 0.15403950705062275
1500 0.14559595572188555
1600 0.13827620932799925
1700 0.1318653873817163
1800 0.12620028791289195
1900 0.1211547117310094
after pred
[ [0.00253563 0.98030863 0.00392367 0.01323207]
[0.00124215 0.00208411 0.98927185 0.00740189]
[0.01060847 0.00131486 0.97464874 0.01342794]
[0.01737727 0.03434559 0.00681429 0.94146284] ]
아주 깔끔하고 올바른 결과가 도출되었다! 이러한 vanishing gradient 문제를 해결하기 위해 LSTM, GRU 방법이 거론되었지만 만족스럽지 못하였고, 2017년 google의 Attention all you need 라는 논문을 통해 Attention 기법이 크게 떠올랐고 아예 rnn 셀이 제거된 transformer 구조가 탄생하여 자연어 인공지능의 새로운 장을 열었다.
RNN은 현재 쓸모없지 않을까? 싶지만 자연어 처리 인공지능의 기본인 만큼 이를 잘 이해한다면 Attention과 Transformer 구조를 잘 이해할 수 있을 것이다.
아래는 전체 코드이다.
import numpy as np
np.random.seed(230912)
dict_heel = {'h':np.array([1, 0, 0, 0]), \
'e':np.array([0, 1, 0, 0]), \
'l':np.array([0, 0, 1, 0]), \
'o':np.array([0, 0, 0, 1]), \
}
# input 값을 설정
inputs = np.array([])
for text in "hell":
for key, value in dict_heel.items():
if key == text:
if inputs.size == 0:
inputs = np.concatenate([inputs, value])
else:
inputs = np.vstack([inputs, value])
input_RNN = np.reshape(inputs, (1, 4 ,-1 ))
# target 값을 설정
target = np.array([])
for text in "ello":
for key, value in dict_heel.items():
if key == text:
if target.size == 0:
target = np.concatenate([target, value])
else:
target = np.vstack([target, value])
targets = np.reshape(target, (1, 4, -1))
time_steps = input_RNN.shape[1] # t.s(4)
sequence_length = input_RNN.shape[2] # s.l(4)
hidden_node = 6 # 내가 설정해야 하는 것, 3에서 6으로 증가
output_feature = targets.shape[1] # o.f(4)
Wxh = np.random.randn(sequence_length, hidden_node) # (s.l(4), h.n(3))
Whh = np.random.randn(hidden_node, hidden_node) # (h.n(3), h.n(3))
Bh = np.random.randn(1, 1) # (1, 1)
Wy = np.random.randn(hidden_node, output_feature) # (h.n(3), o.f(4))
By = np.random.randn(1, 1) # (1, 1)
def rnn_cell(data):
h = np.zeros((1, hidden_node)) #(1, 3) h_-1 상태이며 사실 없으므로 0이다. 반복문을 위해 넣어줌.
# 역전파 계산을 위해 만든 list들
ht_i_list = []
ht_list = []
pred_i_list = []
pred_list = []
ht_list.append(h) # 규칙적인 역전파를 위해 h_-1 상태를 입력함.
count = 0
for sequence in data:
x = np.reshape(sequence, (1, -1))
h_i = np.dot(x, Wxh) + np.dot(h, Whh) + Bh
h = np.tanh(h_i)
pred_i = np.dot(h, Wy) + By
pred = np.exp(pred_i)/np.sum(np.exp(pred_i))
ht_i_list.append(h_i)
ht_list.append(h)
pred_i_list.append(pred_i)
pred_list.append(pred)
if count == 0:
total_pred = pred.copy()
else:
total_pred = np.concatenate([total_pred, pred], axis=0)
count = count + 1
return total_pred, pred_list, pred_i_list, ht_list, ht_i_list
# 오차 계산
def CEE_loss(y_hat, y):
loss = np.sum(-y*np.log(y_hat))
return loss
def loss_gradient(X, Y, lr):
global Wy, By, Wxh, Whh, Bh
dE_dWxh_list = np.zeros_like(Wxh)
dE_dWhh_list = np.zeros_like(Whh)
dE_dBh_list = np.zeros_like(Bh)
#순전파
predics, pred_list, pred_i_list, ht_list, ht_i_list = rnn_cell(X)
# hi_i_list는 [h0_i, h1_i, h2_i, h3_i] 순서
# ht_list는 [h-1, h0, h1, h2, h3] 순서
loss = CEE_loss(predics, Y)
count = 0
for t_s in reversed(range(time_steps)):
# 역전파 실시
dE_dpred_i = pred_list[t_s] - Y[t_s]
#fc 분류기에 대한 기울기 구하기 실시
dpred_i_dWy = np.transpose(ht_list[t_s+1], (1, 0))
dE_dWy = np.dot(dpred_i_dWy, dE_dpred_i)
dE_dBy = np.sum(dE_dpred_i, keepdims=True)
for i in reversed(range(t_s+1)) :
if i == t_s:
dht_plus1_i_dht = np.transpose(Wy, (1, 0))
dE_dth_plus1_i = dE_dpred_i
else:
dht_plus1_i_dht = np.transpose(Whh, (1, 0))
dE_dth_plus1_i = dE_dht_i
dE_dht = np.dot(dE_dth_plus1_i, dht_plus1_i_dht)
dht_dht_i = (1-np.power(np.tanh(ht_i_list[i]), 2))
dE_dht_i = dE_dht * dht_dht_i
# dE_dWxh 구하기
dht_i_dWxh = np.transpose(np.reshape(X[i], (1, -1)), (1, 0)) # (s.l(2), 1)
# X를 그냥 가지고 오면 1차원 배열이여서 2차원으로 바꾸어주어야 함
dE_dWxh = np.dot(dht_i_dWxh, dE_dht_i) # (s.l(2), 1) × (1, h.n(3)) = (s.l(2), h.n(3))
# dE_dWhh 구하기
dht_i_dWhh = np.transpose(ht_list[i], (1, 0)) # (h.n(3), 1)
dE_dWhh = np.dot(dht_i_dWhh, dE_dht_i) # (h.n(3), 1) × (1, h.n(3)) = (h.n(3), h.n(3))
# dE_dBh 구하기
dE_dBh = np.sum(dE_dht_i, keepdims=True) # (1, h.n(3)) -> (1, 1)
# 기울기 누적
dE_dWxh_list += dE_dWxh
dE_dWhh_list += dE_dWhh
dE_dBh_list += dE_dBh
Wy = Wy + -1*lr * dE_dWy
By = By + -1*lr * dE_dBy
Wxh = Wxh + -1*lr * dE_dWxh_list
Whh = Whh + -1*lr * dE_dWhh_list
Bh = Bh + -1*lr * dE_dBh_list
# 훈련 전 예측값
pred, _, _, _, _ = rnn_cell(input_RNN[0])
print('before pred', pred)
for i in range(2000):
loss_gradient(input_RNN[0], targets[0], lr=0.005)
if i % 100 == 0:
pred, _, _, _, _ = rnn_cell(input_RNN[0])
print(i, CEE_loss(pred, targets[0]))
# 훈련 후 예측값
pred, _, _, _, _ = rnn_cell(input_RNN[0])
print('after pred', pred)
3. 마치며
Numpy 딥러닝 시리즈는 당분간 여기에서 멈출 것 같다.
2022년 1월 3일부터 시작하여 23년 9월 24일 RNN을 끝으로 종료하게 되었다. 사실 본업 + 육아로 인해 퇴근하고 나서 밤 10시마다 졸면서(...) 공부하고 작성한 내 자신에게 뿌듯하면서도 성취감을 느낄 수 있었다.(속 시원하다!) 취미로 공부해서 그런지 본업인 물리보다 더 재미있었다는건 안비밀 ㅋㅋㅋㅋ
여기서 다루지 않은 dropout 기법, L1, L2 regularization, 주성분 분석 등 다루어야 할 것은 산더미지만, 딥러닝의 기초를 익히기에는 이 정도면 충분하지 않을까(...) 생각한다. 왜냐면 주 독자를 고등학생, 고등학교를 졸업한지 얼마 안된 1~2학년 대학생 또는 학사 이상의 일반인으로 설정하였기 때문이다. 즉, 이 내용은 개발자들이 공부하는 딥러닝 이론의 '마이너' 이다. 이 글의 목적은 개발자들이 공부하는 딥러닝 이론, 교재가 너무 어렵기 때문에 쉽게 풀어서 설명하기 위해서였다.
그리고 중구난방인 Numpy 딥러닝 시리즈를 정리하여 위키독스(wikidocs)에 다시 작성할 계획이다.
앞으로의 목적은 diffusion 모델과 transformer 구조를 탐구하고 고등학생을 대상으로 수학으로 쉽게 설명하는것이다. 그 때가지 Numpy 딥러닝 시리즈를 탐구한 여러분들께 많은 도움이 되었으면 하는 바램이다. (사실 이걸로 교재도, 책도 쓰고 싶어요... ㅎㅎ)
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| [목차] Numpy 딥러닝 시리즈 (0) | 2023.09.24 |
|---|---|
| 44.[RNN기초] RNN(many to many) 순전파 구현(이론, 실습) (0) | 2023.09.23 |
| 43.[RNN기초] RNN(many to one) 역전파 구현(실습2) (0) | 2023.09.22 |
| 42.[RNN기초] RNN(many to one) 역전파 구현(실습) (0) | 2023.09.20 |
| 41.[RNN기초] RNN(many to one) 역전파 구현(이론) (0) | 2023.09.19 |


