저번시간에 RNN의 순전파의 이론적 배경을 알아보고 코드로 구현하였다.
그렇다면 어떻게 역전파를 진행하여 가중치를 훈련할 수 있을까?
먼저 필요한 변수값을 다시 확인하자
- time steps(t.s) → 3 (문장을 구성하는 토큰의 개수)
- sequence length(s.l) → 2 (데이터 전체의 토큰 개수)
- hidden node(h.n) → 3 (본인이 설정하는 값)
- output feature → 1 (출력 특성)
그리고 가중치의 크기를 확인하자.
- Wxh = ( sequence length(2), hidden node(3) ) → ( 2, 3 )
- Whh = ( hidden node(3), hidden node(3) ) → ( 3, 3 )
- Bh = (1, 1)
- Wy = ( hidden node(3), output feature(1) ) → ( 3, 1 )
- By = (1, 1)
time_steps = input_RNN.shape[1] # t.s(3)
sequence_length = input_RNN.shape[2] # s.l(2)
hidden_node = 3 # 내가 설정해야 하는 것, h.n(3)
output_feature = target.shape[1] # o.f(1)
우리의 목적은 경사하강법을 적용하기 위해 오차에 따른 가중치들의 기울기를 아래와 같이 구해야 한다.

1. 분류기(fc)의 가중치 기울기 구하기
분류기 fc의 가중치에 대한 기울기를 구해보자. 빨간색 화살표 주목

역전파를 진행하기 위해선 Error → Sigmoid(Pred) → fc(pred') 순으로 거꾸로 들어가야 한다.
아래와 같이 Wy와 By는 기존 DNN에서 배웠던 것 처럼 역전파를 실시하면 쉽게 구할 수 있다.
여기서 ∂E / ∂pred'을 미리 정의하고 연산하면 편하다.

2. time step 2 (= h_1, x_2 입력)에서의 가중치 기울기 구하기
h_1과 x_2가 입력되는 time step=2에서의 가ㅋ중치 Wxh, Whh, Bh의 기울기를 구해보자. 빨간색 화살표 주목
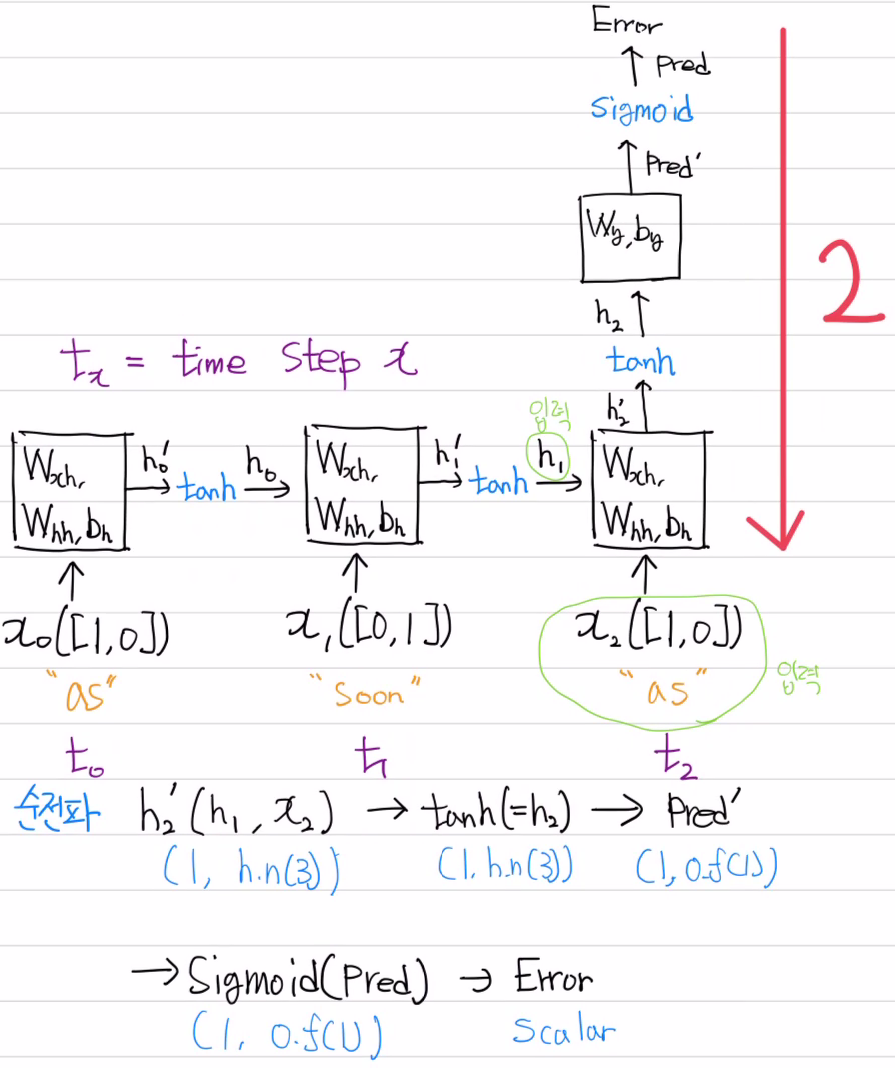
순전파를 참고하여 거꾸로 들어가 time step 2에서의 가중치 기울기 Wxh, Whh, Bh를 구해보자.
과정은 다음과 같다
- fc 분류기 역전파에서 사용하였던 ∂E / ∂pred' 을 가져온다.(주황색 박스)
- fc 분류기에서 기울기를 받아야 한다. 즉 ∂pred' / ∂h_2가 필요하다. 이는 W^(-1)y로 구할 수 있다.
- ∂E / ∂pred'을 이용하여 ∂E_∂h'_2을 정의한다. (노란색 박스)
- ∂E / ∂h'_2를 이용하여 ∂E / ∂Wxh, ∂E / ∂Whh, ∂E / ∂Bh를 차례대로 구한다.

3. time step 1 (= h_0, x_1 입력)에서의 가중치 기울기 구하기
h_0와 x_1이 입력되는 time step=2에서의 가중치 Wxh, Whh, Bh의 기울기를 구해보자. 빨간색 화살표 주목
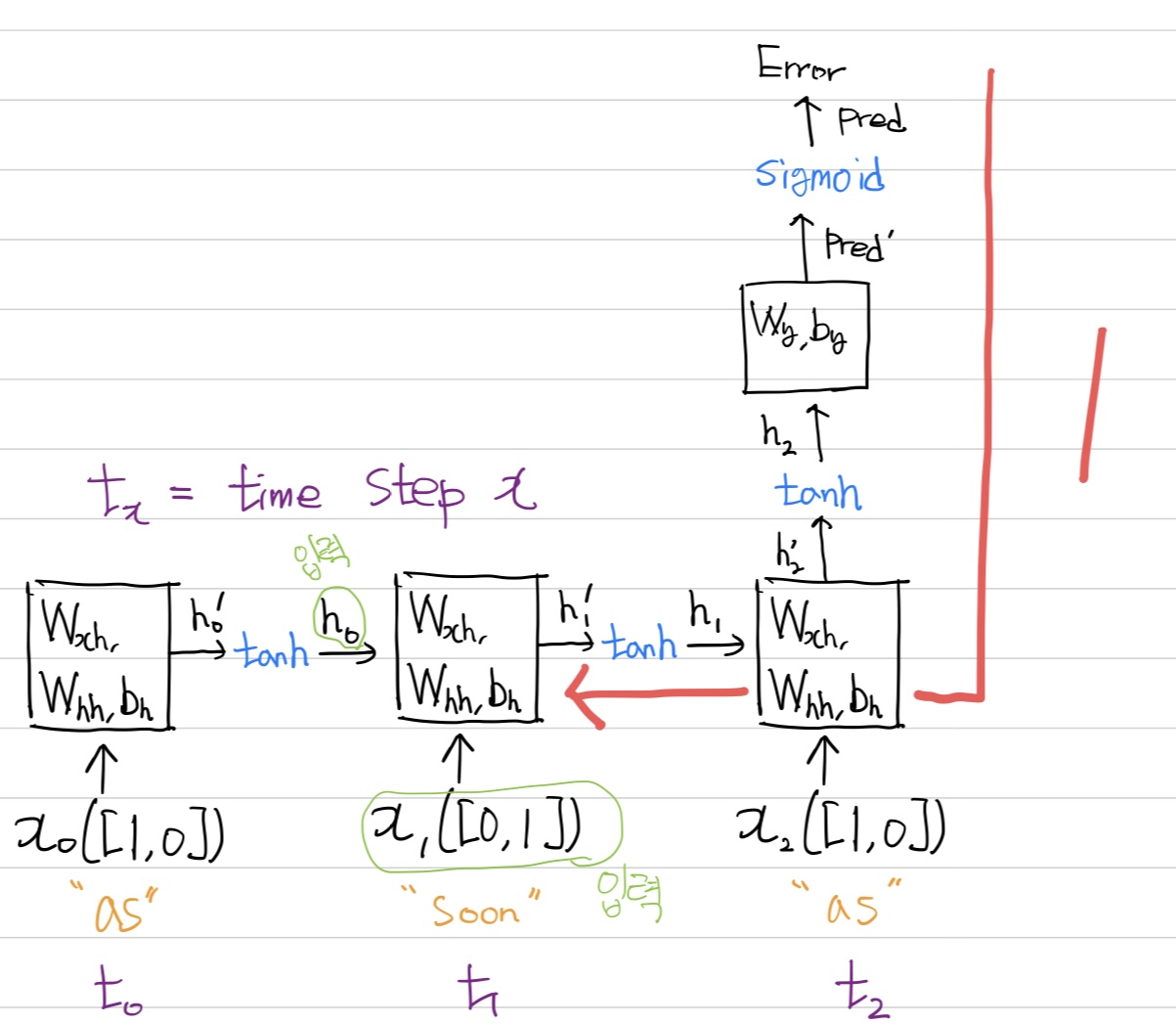
순전파부터 관찰하자. x_1 → x_2로 입력되므로 역전파를 위해서 더 안으로 들어가야 한다.

순전파를 참고하여 거꾸로 들어가 time step 1에서의 가중치 기울기 Wxh, Whh, Bh를 구해보자.
과정은 다음과 같다
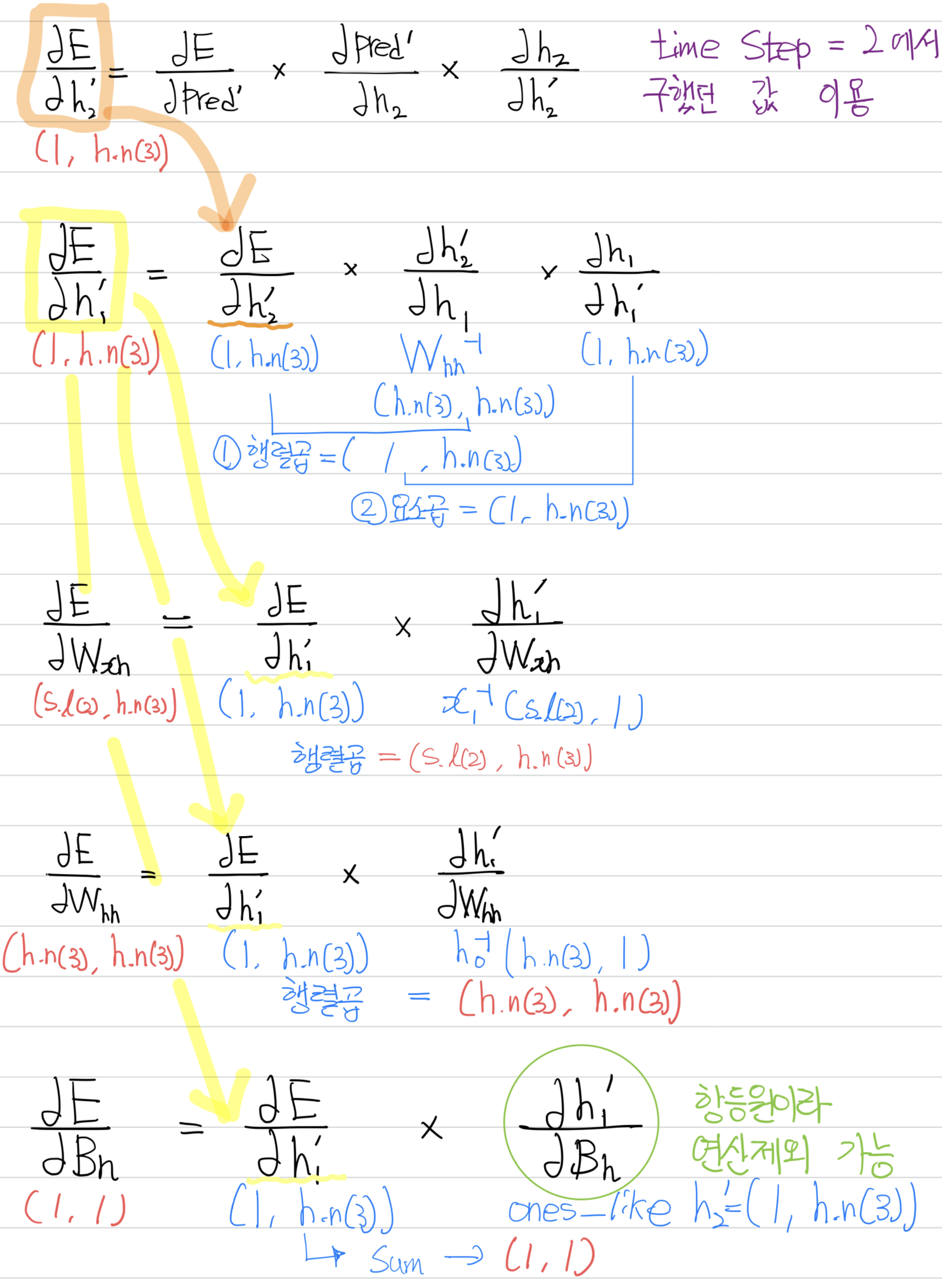
- time step 2 역전파에서 사용하였던 ∂E / ∂h'_2 을 가져온다.(주황색 박스)
- time step 2에서 time step 1으로 기울기를 받아야 한다. 즉 h`_2 → h_1 으로 기울기가 흘러야 하므로 ∂h'_2 / ∂h_1을 구해야 하는데 이는 W^(-1)hh 를 의미한다.
- ∂E / ∂ h'_2 등을 이용하여 ∂E_∂h'_1을 정의한다. (노란색 박스)
- ∂E / ∂h'_1를 이용하여 ∂E / ∂Wxh, ∂E / ∂Whh, ∂E / ∂Bh를 차례대로 구한다.
잘 살펴보면 규칙성이 있음을 학인할 수 있다.
4. time step 0 (= x_1 입력)에서의 가중치 기울기 구하기
x_1이 입력되는 time step=2에서의 가중치 Wxh, Whh, Bh의 기울기를 구해보자. 빨간색 화살표 주목
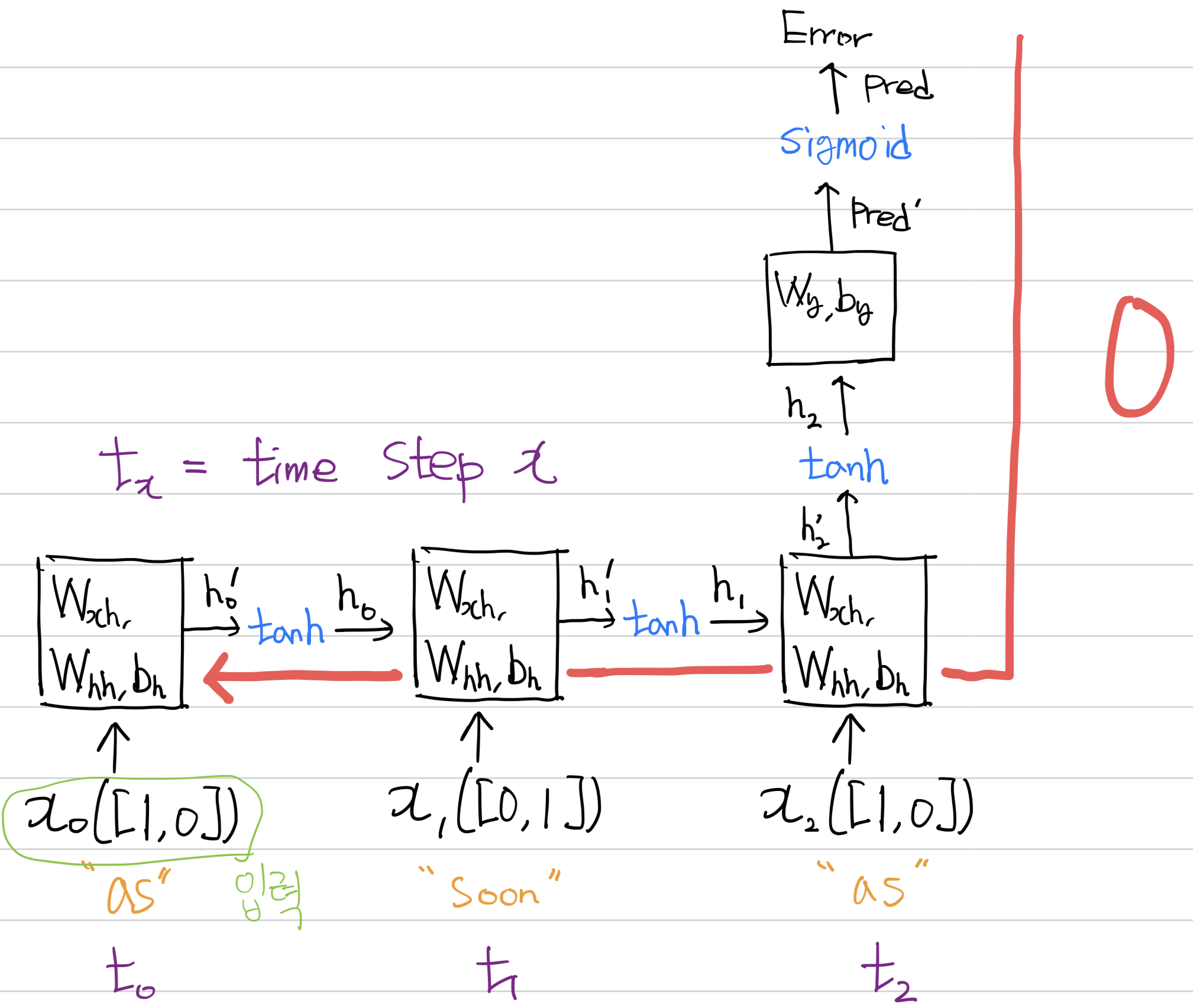
순전파 과정을 다시 살펴보자 x_0 -> x_1 -> x_2 순서와 x_0일 때 이전 은닉 상태 입력이 없음을 잘 살펴보자.

순전파를 참고하여 거꾸로 들어가 time step 0에서의 가중치 기울기 Wxh, Whh, Bh를 구해보자.
과정은 다음과 같다
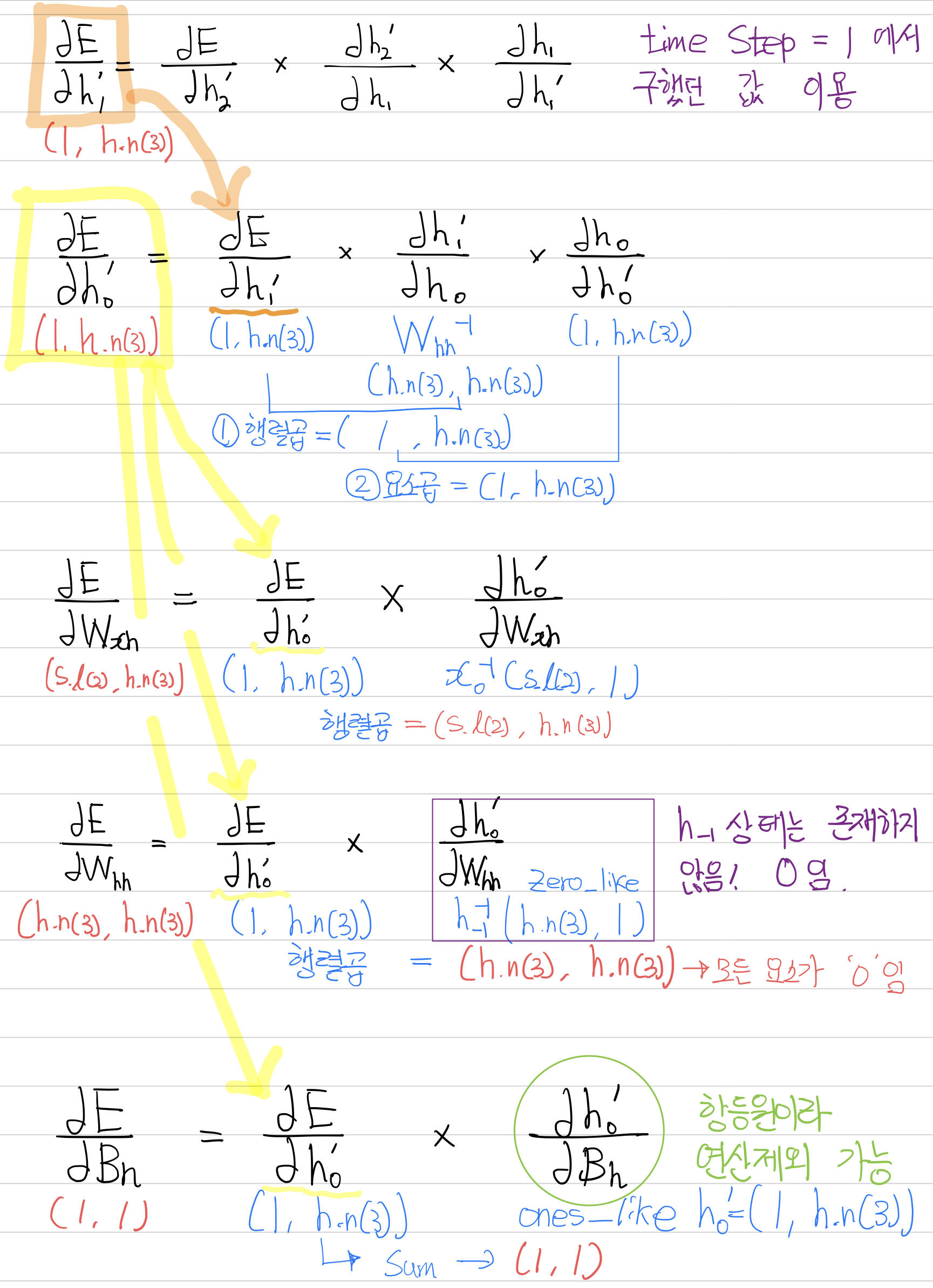
- time step 1 역전파에서 사용하였던 ∂E / ∂h'_1 을 가져온다.(주황색 박스)
- time step 1 에서 time step 0으로 기울기를 받아야 한다. 즉 h`_1 → h_0 으로 기울기가 흘러야 하므로 ∂h'_1 / ∂h_0을 구해야 하는데 이는 W^(-1)hh 를 의미한다.
- ∂E / ∂ h'_1 등을 이용하여 ∂E_∂h'_0을 정의한다. (노란색 박스)
- ∂E / ∂h'_0를 이용하여 ∂E / ∂Wxh, ∂E / ∂Whh, ∂E / ∂Bh를 차례대로 구한다.
- 여기서 ∂E / ∂Whh은 0인데 time step 0 이전 상태(h_-1이라고 하자) 존재하지 않기 때문에 0으로 둔다.
잘 살펴보면 규칙성이 있음을 학인할 수 있다.
fc 분류기 → time step 2 → time step 1 → time step 0 까지 time step 순서의 반대로 역전파를 실시하는데 이를 BPTT(Backpropagation Through Time)이라고 한다. 보면 알겠지만 컴퓨터 자원을 많이 잡아먹는다.
BPTT를 마쳤다면 아래와 같이 기울기를 더하여 누적한다. 이후 경사하강법을 이용하여 가중치를 업데이트한다.

후... 길었다. 다음시간엔 이를 코드로 작성하고 1개의 데이터를 훈련해 보자.
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 43.[RNN기초] RNN(many to one) 역전파 구현(실습2) (0) | 2023.09.22 |
|---|---|
| 42.[RNN기초] RNN(many to one) 역전파 구현(실습) (0) | 2023.09.20 |
| 40.[RNN기초] RNN(many to one) 순전파 구현(실습) (0) | 2023.09.13 |
| 39.[RNN기초] RNN(many to one) 순전파 구현(이론) (0) | 2023.09.12 |
| 38.[RNN기초] 자연어 데이터는 어떻게 접근해야 할까? (0) | 2023.09.11 |



