Pooling을 정말 간단하게 이야기하자면 이미지의 있는 특징들을 요약하는 작업이다. 사용하는 이유는 일반적으로 특성 맵의 차원을 줄임으로써 연산량을 줄여줄 수 있을 뿐만 아니라 특징을 요약했기 때문에 입력 이미지 특징들의 위치 변화(회전, 대칭이동 등)에 잘 반응한다.
Pooling은 최대 풀링(Max pooling)과 평균 풀링(Average pooling) 두 가지가 있는데 각각 장단이 있다.
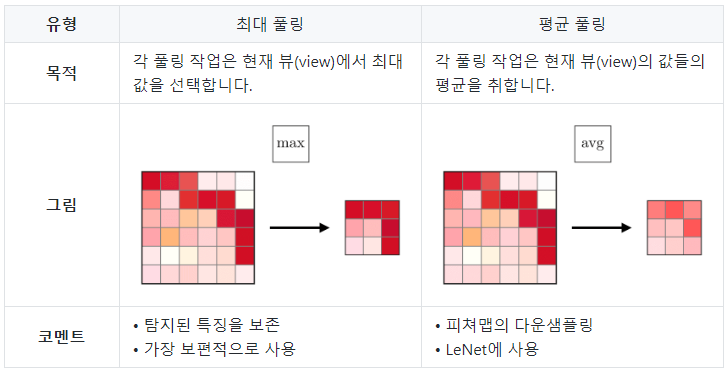
오늘은 풀링을 넘파이로 어떻게 구현하는지 알아보고 다음시간에 풀링층을 적용하여 문제를 해결해 보자.
아래의 1개의 이미지(batch size, height, width)를 풀링해 보자.
# 풀링 레이어 구현 Average Pooling과 Max Pooling을 구현해 보자.
import numpy as np
X = np.array([[[0.1, 0.2, 0.3, 0.4],
[0.5, 0.6, 0.7, 0.8],
[0.9, 1.0, 1.1, 1.2],
[1.3, 1.4, 1.5, 1.6]]])
print(X.shape) # (batch size, height, width) -> (1, 4, 4)
1. 풀링 연산 출력 크기 계산하기
풀링을 실행할 때 출력은 어떻게 계산할 수 있을까? 합성곱 출력을 계산하는 방법을 사용하면 된다. 풀링 연산은 결국 합성곱 연산에서 필터크기의 요소를 다 더하여 1개를 만드는 것이 아닌, 최대 크기 1개를 선택하거나 평균을 반환하는 것이다. 따라서 풀링은 필터 크기 만큼 스트라이드를 실행하고 패딩은 0임을 생각하면 아래와 같은 식을 유도할 수 있다.
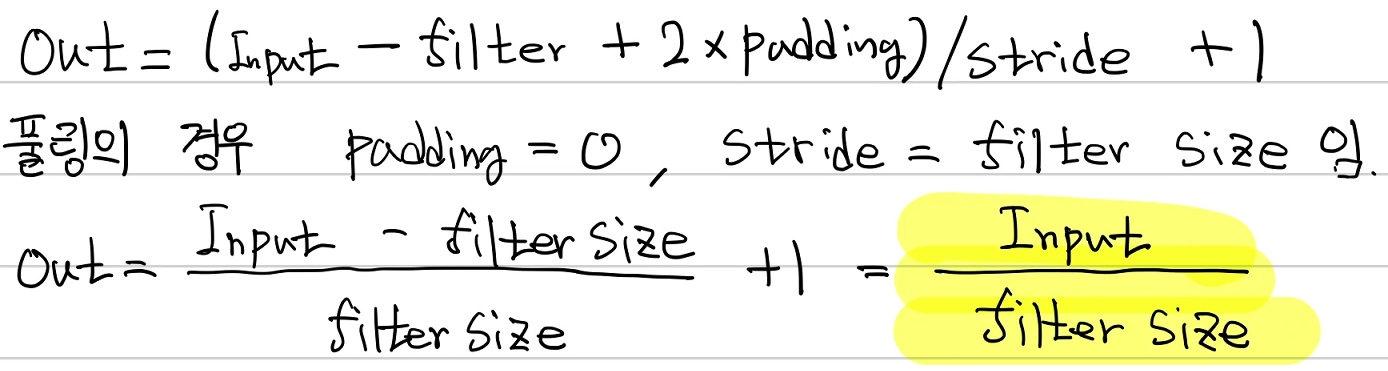
정리하면 풀링 연산의 출력은 (입력 사이즈 / 필터 사이즈)로 간단하게 구할 수 있다.
PADDING = 0
FILTER_SIZE = 2
STRIDE = 2
OUT_SIZE = int(X.shape[1]/FILTER_SIZE) # 2
print(OUT_SIZE)
2. 풀링 연산을 위한 im2col
풀링 연산은 결국 합성곱 연산에서 필터크기의 요소를 다 더하여 1개를 만드는 것이 아닌, 최대 크기 1개를 선택하거나 평균을 반환하는 것이기 때문에 im2col 연산을 이용할 수 있다.
이 때 풀링 연산에서는 일반적으로 패딩을 하지 않기 때문에 padding=0임을 잘 기억하자
def im2col(input, stride, padding, filter_size, output_size):
count = 0
input = np.pad(input, ((padding, padding), (padding, padding)))
for o_h in range(output_size):
for o_w in range(output_size):
a = input[stride*o_h : stride*o_h + filter_size, stride*o_w:stride*o_w + filter_size]
out = np.reshape(a, (1, -1))
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out), axis=0)
count += 1
return np.transpose(outs, (1, 0))
im2col_image = im2col(input=X[0], stride=STRIDE,
filter_size=FILTER_SIZE, output_size=OUT_SIZE)
print(im2col_image)
3. 평균 풀링(Average pooling) 순전파와 역전파
1. 평균 풀링 순전파
평균 풀링을 순전파 해 보자. 과정은 아래와 같다. Conv2D 연산에서 가중치와의 W 연산을 없앤 버전과 거의 동일하다. 그림과 코드를 같이 보자. 평균풀링은 풀링 필터 값들의 평균을 연산하는 과정이다.

def Average_Pooling(inputs, stride, filter_size, output_size):
count = 0
for input in inputs:
im2col_input = im2col(input, stride, 0, filter_size, output_size)
avg_pooling = np.mean(im2col_input, axis=0, keepdims=True)
avg_pooling = np.reshape(avg_pooling, (output_size, output_size))
out = avg_pooling[np.newaxis, :, :]
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out))
count += 1
return outs
Avg_out = Average_Pooling(inputs=X, stride=STRIDE,
filter_size = FILTER_SIZE, output_size = OUT_SIZE)
print(Avg_out)
출력이 3차원인 이유는 batch에 대하여 실행하였기 때문이다.
2. 평균 풀링 역전파
평균 풀링의 역전파를 알아보자. 입력 x에 대한 평균 풀링 연산을 avg_Pooling(x) 라고 할 때 x에 대한 avg_Pooling(x)의 변화율은 어떻게 될까? 아래 연산을 통해 알아보자.

결론은, 평균 풀링연산의 역전파는 입력 이미지의 요소를 필터 요소 개수값으로 나눈 것( 1/N)이 된다. 어떻게 코드로 구현할 수 있는지 그림으로 알아보자.

역전파는 연산의 출력을 이용하여 기울기를 계산하는 것임을 기억하자. np.full을 이용하여 im2col 연산 출력 크기 만큼의 행렬을 필터 가중치 개수(N)를 나눈 값(1/N)으로 채우고 col2im으로 하여 다시 이미지 크기로 돌리면 된다.
마찬가지로 패딩 연산을 하지 않았으므로 padding=0이다.
def col2im(input, stride, padding, filter_size, output_size, origin_size):
input = np.transpose(input, (1, 0)) # col로 된 것을 다시 row로 바꿈
input = np.reshape(input, (-1, filter_size, filter_size)) # row로 된 것을 다시 필터 크기로 바꾸어준다.
output = np.zeros((origin_size, origin_size)) # 원래 이미지 크기의 0 행렬을 만들어 준다.
index = 0
for o_h in range(output_size):
for o_w in range(output_size):
output[stride*o_h : stride*o_h + filter_size, stride*o_w:stride*o_w + filter_size] = input[index] # input2row의 역연산을 수행
index += 1
if padding == 0:
pass
else:
for i in range(padding): # 패딩 제거 작업
output = np.delete(output, 0, axis=0) # 맨 윗 줄 없앰
output = np.delete(output, (output.shape[0]-1), axis=0) # 맨 아래줄 없앰
output = np.delete(output, 0, axis=1) # 맨 앞 줄 없앰
output = np.delete(output, (output.shape[1]-1), axis=1) # 맨 뒷줄 없앰
return output
def backward_Avg_Pooling(inputs, stride, filter_size, output_size, origin_size):
for count in range(inputs.shape[0]):
grad_avg_Pooling = np.full((filter_size*filter_size, output_size*output_size), 1/(filter_size*filter_size))
grad_avg_col2im = col2im(grad_avg_Pooling, stride, 0, filter_size, output_size, origin_size)
out = grad_avg_col2im[np.newaxis, :, :]
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out))
count += 1
return outs
back_avg = backward_Avg_Pooling(inputs=Avg_out, stride=STRIDE,
filter_size = FILTER_SIZE, output_size=OUT_SIZE,
origin_size=X.shape[1])
print(back_avg)
4. 최대 풀링(Max pooling) 순전파와 역전파
1. 최대 풀링 순전파
최대 풀링을 순전파 해 보자. 과정은 아래와 같다. 마찬가지로 Conv2D 연산에서 가중치와의 W 연산을 없앤 버전과 거의 동일하다. 이미지에서 최대 풀링을 많이 이용하므로 이 과정을 잘 이해하는 것이 좋다. 다음 시간에 최대 풀링을 이용하여 훈련할 것이다. 최대 풀링은 풀링 필터 크기 구역에서 최대값 1개를 선택하는 과정이다.

이를 코드로 표현하면 아래와 같다. np.max를 이용하여 1개의 열에서 최대값을 선택하여 리턴하게 만들면 된다.
def Max_Pooling(inputs, stride, filter_size, output_size):
count = 0
for input in inputs:
im2col_input = im2col(input, stride, 0, filter_size, output_size)
max_pooling = np.max(im2col_input, axis=0, keepdims=True)
max_pooling = np.reshape(max_pooling, (output_size, output_size))
out = max_pooling[np.newaxis, :, :]
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out))
count += 1
return outs
Max_out = Max_Pooling(inputs=X, stride=STRIDE,
filter_size = FILTER_SIZE, output_size = OUT_SIZE)
print(Max_out)
2. 최대 풀링 역전파
최대 풀링의 역전파를 알아보자. 입력 x에 대한 최대 풀링 연산을 Max_Pooling(x) 라고 할 때 x에 대한 Max_Pooling(x)의 변화율은 어떻게 될까? 아래 연산을 통해 알아보자.

결론은, 최대 풀링의 역전파는 입력 이미지의 최대값은 1, 그 외 나머지는 0이 된다. 전체 과정을 그림으로 알아보자. 이 때문에 Max pooling 연산 전 이미지가 필요하다.

이를 코드로 표현하면 아래와 같다. max pooling의 연산 결과를 재입력 해야 하므로 이를 inputs, max pooling 연산을 행할 이미지 정보가 필요하므로 이를 origins라 하였다. zip을 이용해 동시에 for문을 순회한다.
np.where를 이용해 일치하면 1 아니면 0을 구현하였다.
def backward_Max_Pooling(inputs, origins, stride, padding, filter_size, output_size, origin_size):
count = 0
for input, origin in zip(inputs, origins):
input = np.reshape(input, (1, -1))
repeat_max_pooling = np.tile(input, reps=[filter_size*filter_size, 1])
origin_im2col = im2col(origin, stride, 0, filter_size, output_size)
grad_max_pooling = np.where(input==origin_im2col, 1, 0)
grad_max_col2im = col2im(grad_max_pooling, stride, padding, filter_size, output_size, origin_size)
out = grad_max_col2im[np.newaxis, :, :]
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out))
count += 1
return outs
back_max = backward_Max_Pooling(inputs=Max_out, origins=X, stride=STRIDE,
filter_size = FILTER_SIZE,
output_size = OUT_SIZE, origin_size = X.shape[1])
print(back_max)
'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 36. [CNN기초] 원, 네모를 구별하는 CNN 만들기(실습) (2) | 2023.02.01 |
|---|---|
| 35. [CNN기초] 원, 네모를 구별하는 CNN 만들기(이론) (2) | 2023.01.28 |
| 33. [CNN기초] 이미지의 합성곱 훈련 -쉬운예제(실습)- (0) | 2023.01.21 |
| 32. [CNN기초] 이미지의 합성곱 훈련 -쉬운예제(이론)- (0) | 2023.01.20 |
| 31. [CNN기초] 2차원 배열 합성곱 - image to column-2 (0) | 2023.01.11 |



