이번 시간에는 2017년 서울의 1년 평균 기온 그래프를 분석하고 numpy를 이용해 표현하는 방법을 알아볼 것이다.
이 글을 처음 읽는다면 지수가중이동평균(Exponentially Weighted Moving Average)-1 을 먼저 읽고 오길 바란다. (같이 보면서 읽는다면 더 좋다)
위 자료는 Daily Temperature of Major Cities 라는 자료에서 발췌한 것이다.
1. 데이터 확인
위 자료를 내려받고 임포트한 다음 matplotlib로 그려보자. 코드는 아래와 같다.
import numpy as np
import matplotlib.pyplot as plt
from numpy import genfromtxt
data = genfromtxt('2017_seoul_temperature-2C.csv', delimiter=',', skip_header=1)
days = data[:, 0]
temp = data[:, 1:]
plt.plot(days, temp, 'ro', markersize=3, label='original')
plt.xlabel('days')
plt.ylabel('temperature')
plt.legend()
plt.show()
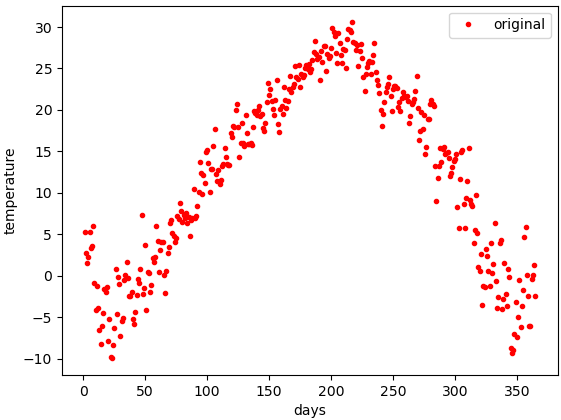
여름이라도 8월 한달 동안 온도는 같지 않다. 위 데이터를 보면서 알 수 있는 사실은 같은 계절, 같은 달이어도 어느 정도 편차가 존재한다는 것을 알 수 있다.
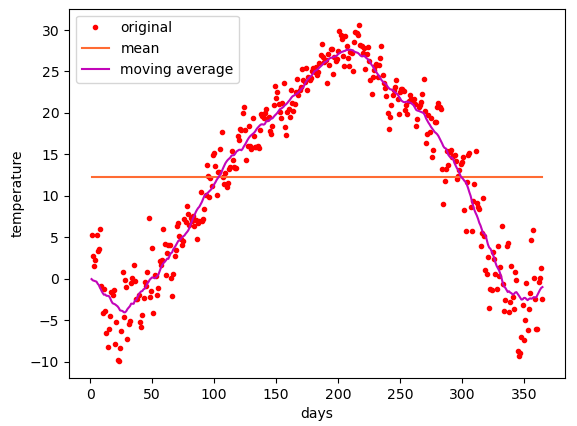
2. 평균(Average)
위 값을 단순 평균을 내린다면 어떤 일이(대참사가) 일어날까?
np.mean을 이용하여 평균을 구할 수 있고 이 값을 그래프에 그리기 위해 np.repeat을 이용하여 배열에 반복하여 입력한다.
import numpy as np
import matplotlib.pyplot as plt
from numpy import genfromtxt
data = genfromtxt('2017_seoul_temperature-2C.csv', delimiter=',', skip_header=1)
days = data[:, 0]
temp = data[:, 1:]
means = np.repeat(np.mean(temp), len(temp))
plt.plot(days, temp, 'ro', markersize=3, label='original')
plt.plot(days, means, color='#FF6B33', markersize=3, label='mean')
plt.xlabel('days')
plt.ylabel('temperature')
plt.legend()
plt.show()

3. 이동평균(Moving Average)
저번 예시에서 사용한 이동평균을 이용해 보겠다. 한 달은 대략 30일 이니까 30개씩 묶어서 평균을 내보겠다. 이 코드를 작성하기 위해
(2) https://runebook.dev/ko/docs/numpy/reference/generated/numpy.convolve
두 곳을 참고하였다. numpy convolve로 내적을 할 수 있다.
import numpy as np
import matplotlib.pyplot as plt
from numpy import genfromtxt
data = genfromtxt('2017_seoul_temperature-2C.csv', delimiter=',', skip_header=1)
days = data[:, 0]
temp = data[:, 1:]
means = np.repeat(np.mean(temp), len(temp))
moving_avg = np.convolve(temp.flatten(), np.ones(30), 'same')/30
plt.plot(days, temp, 'ro', markersize=3, label='original')
plt.plot(days, means, color='#FF6B33', markersize=3, label='mean')
plt.plot(days, moving_avg, color='#C205B9', markersize=3, label='moving average')
plt.xlabel('days')
plt.ylabel('temperature')
plt.legend()
plt.show()
4. 가중이동평균(Weighted Moving Average)
저번시간에 설명했던 가중이동평균을 사용해 보겠다. 가중치는 1단위로 감소하는 단조이다. 마찬가지로 30일 단위로 평균을 내 보겠다.
import numpy as np
import matplotlib.pyplot as plt
from numpy import genfromtxt
data = genfromtxt('2017_seoul_temperature-2C.csv', delimiter=',', skip_header=1)
days = data[:, 0]
temp = data[:, 1:]
means = np.repeat(np.mean(temp), len(temp))
moving_avg = np.convolve(temp.flatten(), np.ones(30), 'same')/30
weighted_moving_avg = np.convolve(temp.flatten(), np.arange(1, 31), 'same')/np.sum(np.arange(1, 31))
plt.plot(days, temp, 'ro', markersize=3, label='original')
plt.plot(days, means, color='#FF6B33', markersize=3, label='mean')
plt.plot(days, moving_avg, color='#C205B9', markersize=3, label='moving average')
plt.plot(days, weighted_moving_avg, color='#39C205', markersize=3, label='weighted moving average')
plt.xlabel('days')
plt.ylabel('temperature')
plt.legend()
plt.show()
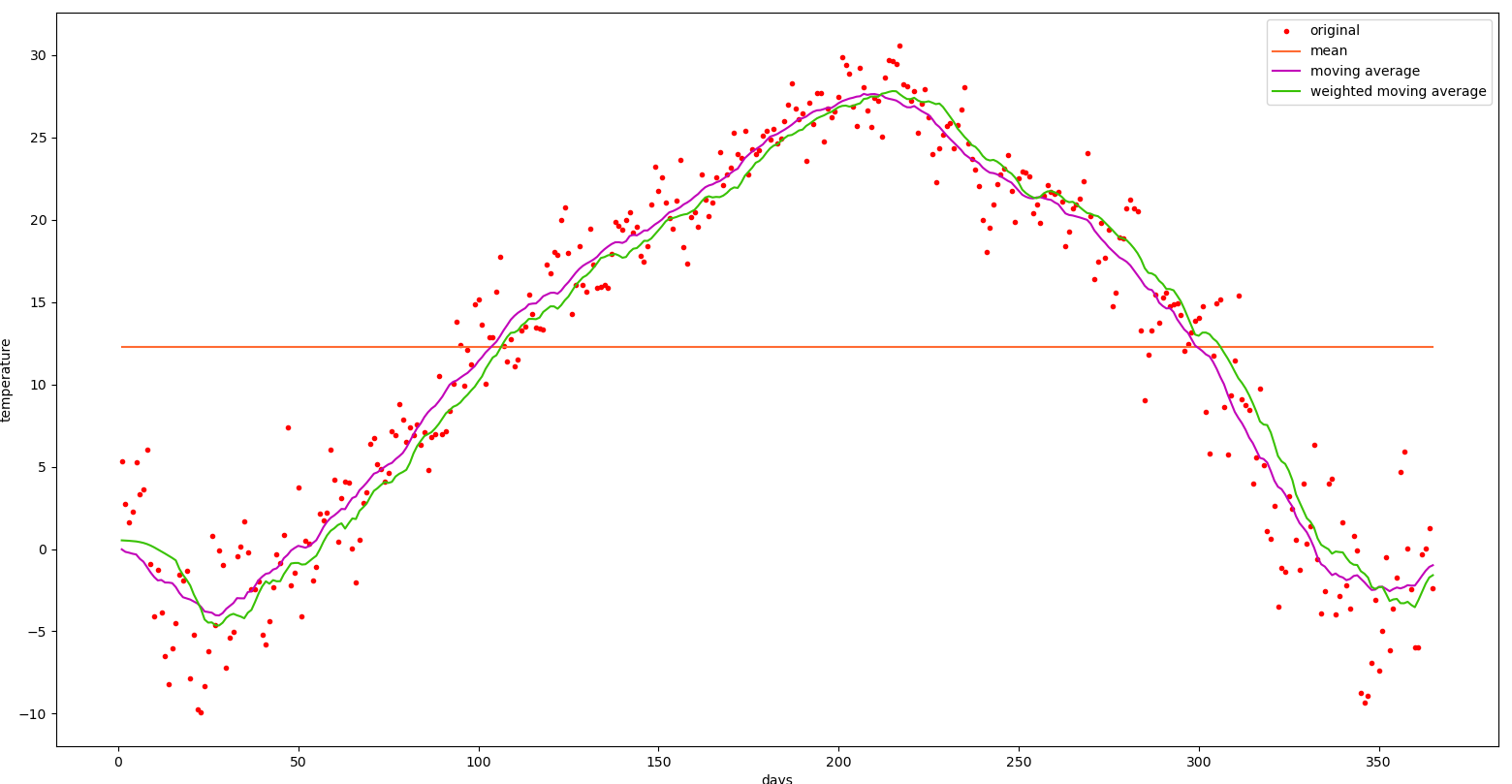
초록색이 가중이동평균이다. 계산 과정에서 최근의 데이터에 가중값을 크게(30) 두었기 때문에 그래프가 전체적으로 이동평균(보라색)보다 앞으로 전진해 있는 것처럼 보인다.
5. 지수가중이동평균(Exponentially Weighted Moving Average) EWMA
이번에는 지수가중이동평균을 사용해 보겠다. α이 0.5, 0.9, 0.99 일 때 그래프이다.
import numpy as np
import matplotlib.pyplot as plt
from numpy import genfromtxt
data = genfromtxt('2017_seoul_temperature-2C.csv', delimiter=',', skip_header=1)
days = data[:, 0]
temp = data[:, 1:]
alpha_05 = 0.5
alpha_09 = 0.9
alpha_099 = 0.99
EWMA_05 = []
EWMA_09 = []
EWMA_099 = []
for i in range(len(days)):
if i == 0:
Y = temp[0]
else:
Y = alpha_05*Y+(1-alpha_05)*temp[i]
EWMA_05.append(Y[0])
for i in range(len(days)):
if i == 0:
Y = temp[0]
else:
Y = alpha_09*Y+(1-alpha_09)*temp[i]
EWMA_09.append(Y[0])
for i in range(len(days)):
if i == 0:
Y = temp[0]
else:
Y = alpha_099*Y+(1-alpha_099)*temp[i]
EWMA_099.append(Y[0])
means = np.repeat(np.mean(temp), len(temp))
moving_avg = np.convolve(temp.flatten(), np.ones(30), 'same')/30
weighted_moving_avg = np.convolve(temp.flatten(), np.arange(1, 31), 'same')/np.sum(np.arange(1, 31))
plt.plot(days, temp, 'ro', markersize=3, label='original')
plt.plot(days, means, color='#FF6B33', markersize=3, label='mean')
plt.plot(days, moving_avg, color='#C205B9', markersize=3, label='moving average')
plt.plot(days, weighted_moving_avg, color='#39C205', markersize=3, label='weighted moving average')
plt.plot(days, EWMA_05, color='#D1F529', markersize=3, label='EWMA 0.5')
plt.plot(days, EWMA_09, color='#000000', markersize=3, label='EWMA 0.9')
plt.plot(days, EWMA_099, color='#253F85', markersize=3, label='EWMA 0.99')
plt.xlabel('days')
plt.ylabel('temperature')
plt.legend()
plt.show()
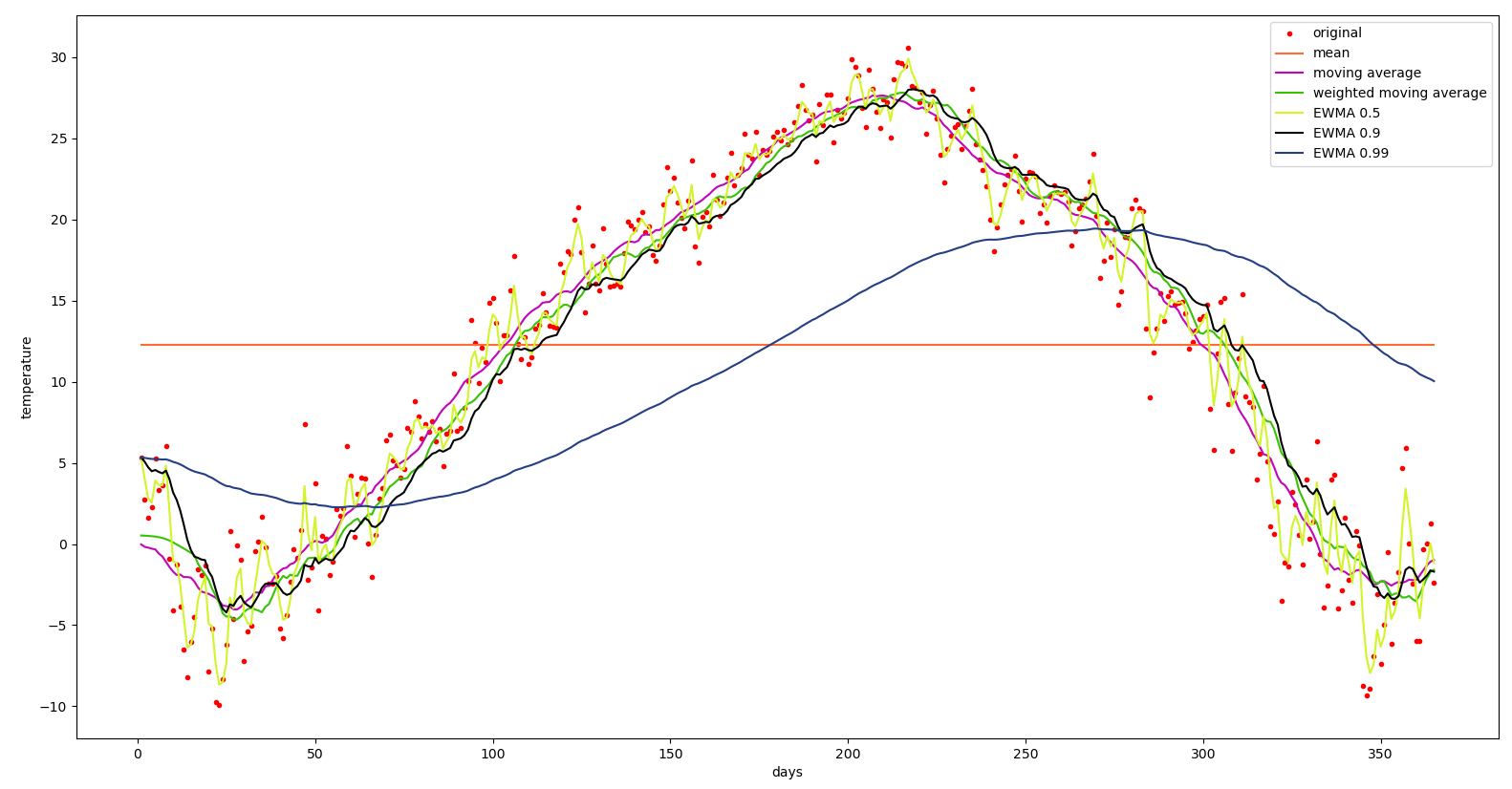
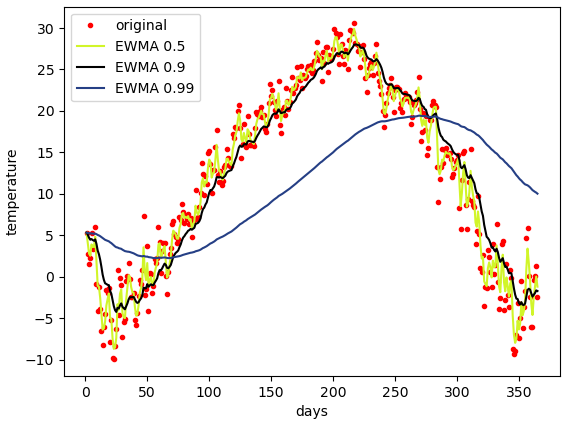
α = 0.5일때 오래된 값의 감쇠가 충분히 일어나지 않아 데이터가 진동하는 것으로 보인다(노란색 그래프)
α = 0.9일때 데이터를 이동평균한 것 같은 모양이 보이고(검은색 그래프)
α = 0.99일 때 오래된 값이 빠른 감쇠가 되어 데이터가 밀려서 생성되는 듯한 모양이 보인다.(남색 그래프)
재미있는 공식이 있는데 1 / (1 - α) 값은 해당 값까지의 지수가중이동평균값에 근사한다는 것이다.
예를 들어보면 α = 0.5 일 때 1/(1-α) = 2이고 이는
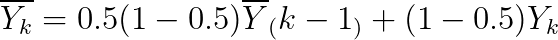
α = 0.9 일 때 1/(1-α) = 10 이고 이는
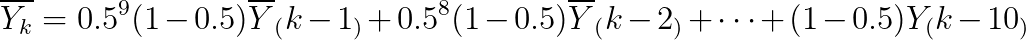
α = 0.99 일 때 1/(1-α) = 100 이고 이는
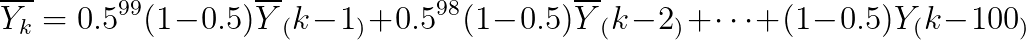
에 각각 근사한다. (증명은 생략한다.) 데이터가 어디까지 더해질 지 예상 가능하므로 지수가중이동평균 그래프의 경향을 대략 유추할 수 있다.
경사하강법에서 위 개념을 어떻게 적용하는지 보여줄 것이다.
'파이썬 프로그래밍 > 딥러닝과 수학' 카테고리의 다른 글
| 평균, 분산, 표준편차, 정규화, 표준화 (0) | 2022.03.02 |
|---|---|
| 지수가중이동평균(Exponentially Weighted Moving Average)-1 (2) | 2022.01.24 |
| 7. 2차원 행렬을 입력받는 합성함수의 도함수(실습) (0) | 2021.12.31 |
| 6. 2차원 행렬을 입력받는 합성함수의 도함수(이론) (0) | 2021.12.31 |
| 5. 벡터 합성함수의 도함수 표현 (0) | 2021.12.29 |



