이전 28번 구현에서 3개의 배치가 있는 경우 훈련 결과가 상당히 좋지 않았다.
노란색 부분이 1, 그 외에는 0이 되어야 하는데 완벽하지가 않다.
무엇이 문제이고 어떻게 해결할 수 있을까? 여러 가지 방법이 있으며 하나씩
살펴보기로 하자.

1. 패딩 구현하기
첫 번째 이유로 합성곱 시 입력 데이터를
균등하게 사용하지 않을 수 있기 때문이다.
아래 그림을 살펴보자.

합성곱 과정을 살펴보면
양 끝단 자료일 수록 합성곱 횟수가 감소한다.
이에 정확한 특성맵을 작성하기 힘들 수 있다.
이를 해결하기 위해 패딩(Padding)을 사용해 볼 수 있다.
패딩은 입력 데이터 주변에 특정 값으로 채우는 것을 의미한다.
우리는 모든 입력 요소가 균등하게 연산되게 하고 싶으므로
양 끝단을 각각 2개의 0의 요소로 채우는 것을 생각해 볼 수 있다.

0으로 패딩(제로 패딩)을 한다면
0과 합성곱 필터 요소와 곱하여 다시 0이 되기 때문에
원래 입력 요소에 영향을 주지 않게 만들 수 있다.
아래 과정을 살펴보자.

넘파이는 pad 메서드를 아래와 같이 지원한다.

우리는 좌, 우에 각 2개씩 적용하고 싶으므로 아래와 같이 코드를 작성할 수 있다.
X = np.pad(X, ((0, 0), (2, 2)))
패딩을 추가하게 되면 특성맵 출력 개수는 아래와 같이 계산되어 바뀐다.

2. 선형 연산 추가하기
합성곱 결과를 바로 학습 목표값(pred)로 하지 않는 것이 좋다.
왜냐하면 합성곱 결과인 특성맵은 이미지의 특징을 담고 있는 것이지
학습 결과가 아니기 때문이다.
즉, 특성맵은 부호화(encoding)되었다고 표현한다.
(부호화를 간단하게 컴퓨터가 이미지 특징을 이해하는 과정(?)
이라고 생각하면 좋을 듯 싶다.)
따라서 부호화된 특성맵을 바탕으로 정보를 이끌어내야 한다.
이 과정에서 필요한 것이 선형 연산을 사용하는
fully connected layer (fc layer)이다.
선형 회귀 과정을 한번 더 거친다고 과감하게 생각해 볼 수 있다.
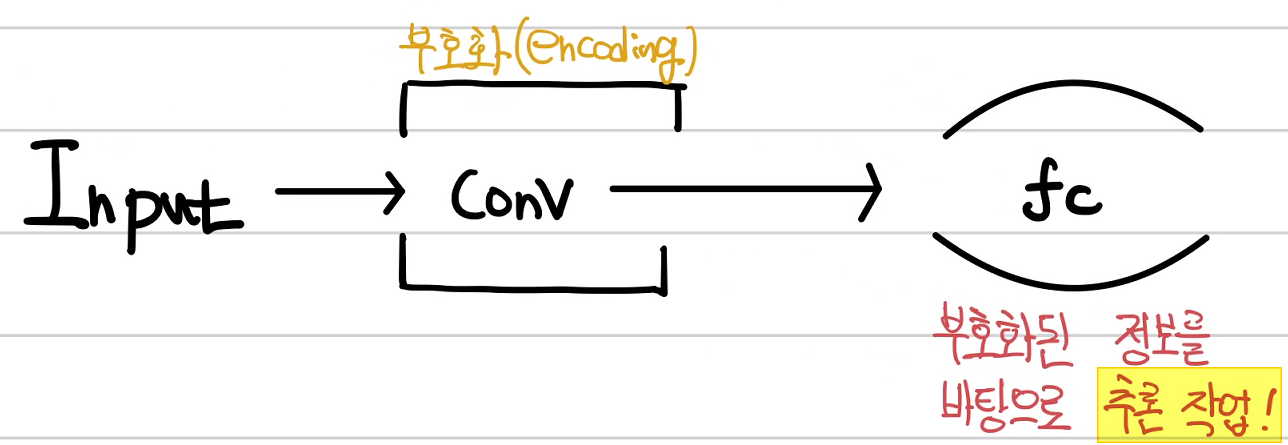
여기에 출력을 sigmoid로 하여 0~1 사이로 정규화를 생각해 볼 수 있다.
이렇게 하기 위해 목표값인 Y를 아래와 같이 변경한다.

왼쪽에 1이 있을 수록 1,
오른쪽에 1이 있다면 0으로 설정하여
가운데가 1인 경우 0.5로 설정하였다.
이에 따라 입력 X, 목표 Y, X 패딩, 특성맵 너비(fmap_width) 등
훈련을 위한 초기값 설정을 아래와 같이 하고
결과를 확인해 보자.

3. 코드 수정하기
1) 합성곱 함수 수정하기
합성곱만 수행했던 forward 함수는 이제 합성곱 외에도
다른 연산도 수행한다. 따라서 이전에 작성했던 함수 2개를
통합해야 더 깔끔하게 작성할 수 있다.

수정된 합성곱 함수는 위의 두 함수를 합친 것이다.
def Conv1D(inputs, weight, bias):
count = 0
for input in inputs:
conv = np.zeros(fmap_width,)
for i in range(fmap_width):
a = 0
for j in range(weight.shape[0]):
a += input[j+i]*weight[j]
conv[i] = a
conv = conv + bias
out = conv[np.newaxis, :]
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out))
count += 1
return outs
2) 합성곱 역전파 함수 수정하기
마찬가지로 이전 예제에서 자세한 설명을 위해
나누었던 gradient_conv와 backward_conv 두 함수를 합쳐
하나의 gradient_conv로 작성하자.

수정된 합성곱 역전파 함수는 두 함수를 합친 것이다.
def gradient_conv (inputs, weight):
count = 0
for input in inputs:
grad_conv = np.zeros(weight.shape[0],)
for i in range(weight.shape[0]):
a = 0
for j in range(fmap_width):
a += input[j+i]
grad_conv[i] = a
out = grad_conv[np.newaxis, :]
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out))
count += 1
return outs
4. 순전파 정의하기
위에서 제시한 방법을 추가하여 순전파를 아래와 같이 정의할 수 있다.

이에 따라 합성곱 가중치와 선형 연산 가중치를 다음과 같이 설정해야 한다.
# 합성곱 연산 가중치 설정
Wc = np.random.randn(3, )
Bc = np.random.randn(1, )
# 선형 연산 가중치 설정
Wl = np.random.randn(1, 7)
Bl = np.random.randn(1, 1)
위에 제시된 대로 순전파 함수 forward를 작성해 보자.
주석으로 작성한 shape과 그림에서 제시된 shape을
비교하여 보자.
마지막 loss는 오차함수로 이진 교차 엔트로피
Binary Cross Entrophy를 사용하였다.
def forward(inputs, target):
# 합성곱 실시
conv = Conv1D(X, Wc, Bc) # (batch, 7)
# linear 연산 Fully connectied
conv = np.transpose(conv, (1, 0)) # (7, batch)
fc = np.dot(Wl, conv) + Bl # (1, 7) * (7, batch ) + (1, 1) = (1, batch)
# 시그모이드 함수 통과 -> (1, batch)
pred = 1 / (1 + np.exp(-fc))
Y = np.transpose(target, (1, 0)) # target(batch, 1) -> (1, batch)
loss = np.sum(-Y*np.log(pred) - (1-Y)*np.log(1-pred))
return loss, pred, fc, conv
5. 역전파 정의하기
대망의 역전파다. 역전파를 이용하여 오차 L에 대한 가중치 W, 편향 B에 대한
기울기를 구하여야 한다.
1) 선형 연산 가중치 Wl과 편향 Bl

2) 합성곱 연산 가중치 Wc와 편향 Bc
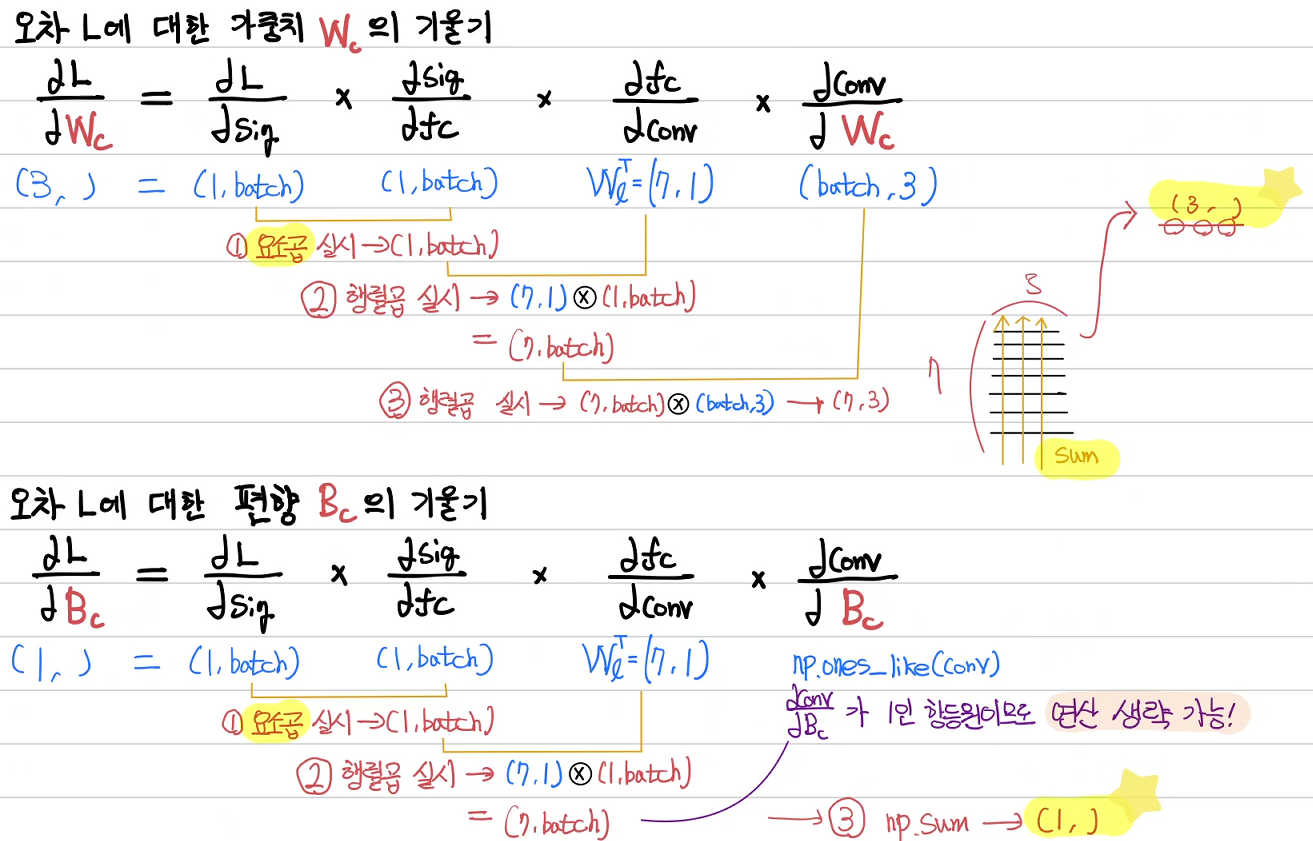
이를 코드로 작성하여 보자
오차에 대한 가중치와 편향의 기울기를 구하는
loss_gradient 함수이다.
마찬가지로 위 그림에서 표시한 shape과
주석으로 표시한 shape을 잘 살펴보아야 한다.
def loss_gradient(inputs, targets):
_, pred, fc, conv = forward(inputs, targets) # _, (1, batch), (1, batch), (7, batch)
Y = np.transpose(targets, (1, 0)) # (batch, 1) -> (1, batch)
dL_dsig = -1*( (Y / pred) - ( (1-Y) / (1-pred) ) ) # (1, batch)
#print(dL_dsig)
dsig_dfc = ( 1/(1+np.exp(-fc)) ) * ( 1 - 1/(1+np.exp(-fc)) ) # (1, batch)
#print(dsig_dfc)
dfc_dWl = np.transpose(conv, (1, 0)) # (batch, 7)
#print(dfc_dWl)
# dfc_dBl = np.ones_like(fc) (1, batch) 어차피 1인 요소인 항등원이므로 없어도 무방합니다.
# Wl, Bl 을 구해봅시다.
dL_dfc = dL_dsig * dsig_dfc # (1, batch)
# print(dL_dfc)
dL_dWl = np.dot(dL_dfc, dfc_dWl) # (1, 7)
#print(dL_dWl)
dL_dBl = np.sum(dL_dfc, keepdims=True) # (1, 1)
#print(dL_dBl)
dfc_dconv = np.transpose(Wl, (1, 0)) # (7, 1)
#print(dfc_dconv)
dconv_dWc = gradient_conv(inputs, Wc) # (batch, 3)
#print(dconv_dWc)
# dconv_dWc = np.ones_like(np.transpose(conv, (1, 0)))
# conv의 원래 형태인 (batch, 7)에서 1인 요소인 항등원이므로 없어도 무방
# Wc, Bc 를 구해봅시다.
dL_dconv = np.dot(dfc_dconv, dL_dfc) # (7, batch)
#print(dL_dconv)
dL_dWc = np.sum(np.dot(dL_dconv,dconv_dWc), axis=0) # (3, )
#print(dL_dWc)
dL_dBc = np.sum(dL_dconv)
#print(dL_dBc)
return dL_dWl, dL_dBl, dL_dWc, dL_dBc
6. 훈련 및 결과 확인하기
경사하강법을 적용하여 아래와 같이 훈련해 보았다.
결과는 어떠하였을까?
learning_rate = 0.05
epochs = 600
for epoch in range(epochs+1):
dL_dWl, dL_dBl, dL_dWc, dL_dBc = loss_gradient(X, Y)
Wl = Wl + -1*learning_rate*dL_dWl
Bl = Bl + -1*learning_rate*dL_dBl
Wc = Wc + -1*learning_rate*dL_dWc
Bc = Bc + -1*learning_rate*dL_dBc
if epoch % 60 == 0:
loss, pred, _, _ = forward(X, Y)
print('epoch :', epoch, '\n', 'pred :' , pred, '\n', 'loss :', loss)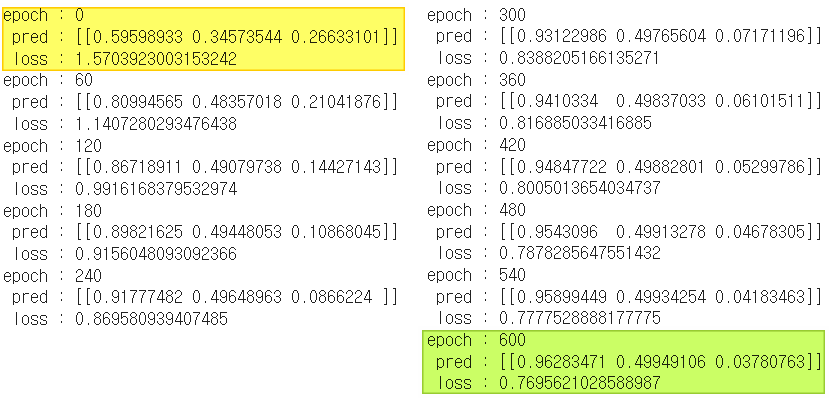
마지막 초록색 pred를 보면 알 수 있듯이
각 1, 0.5, 0에 가깝게 수렴한 것을
알 수 있다.
아래는 전체 코드이다.
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(221222)
X = np.array([[1., 0.7, 0.5, 0.3, 0.1],
[0.5, 0.7, 1, 0.7, 0.5],
[0.1, 0.3, 0.5, 0.7, 1.]])
Y = np.array([[1],
[0.5],
[0.]])
X = np.pad(X, ((0, 0), (2, 2)))
fmap_width = 7 # ((5-3+2*2)/1 + 1)
plt.imshow(X, cmap='gray')
plt.show()
# 합성곱 연산 가중치 설정
Wc = np.random.randn(3, )
Bc = np.random.randn(1, )
# 선형 연산 가중치 설정
Wl = np.random.randn(1, 7)
Bl = np.random.randn(1, 1)
def Conv1D(inputs, weight, bias):
count = 0
for input in inputs:
conv = np.zeros(fmap_width,)
for i in range(fmap_width):
a = 0
for j in range(weight.shape[0]):
a += input[j+i]*weight[j]
conv[i] = a
conv = conv + bias
out = conv[np.newaxis, :]
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out))
count += 1
return outs
def forward(inputs, target):
# 합성곱 실시
conv = Conv1D(X, Wc, Bc) # (batch, 7)
# linear 연산 Fully connectied
conv = np.transpose(conv, (1, 0)) # (7, batch)
fc = np.dot(Wl, conv) + Bl # (1, 7) * (7, batch ) + (1, 1) = (1, batch)
# 시그모이드 함수 통과 -> (1, batch)
pred = 1 / (1 + np.exp(-fc))
Y = np.transpose(target, (1, 0)) # target(batch, 1) -> (1, batch)
loss = np.sum(-Y*np.log(pred) - (1-Y)*np.log(1-pred))
return loss, pred, fc, conv
# 합성곱의 기울기 구하기
def gradient_conv (inputs, weight):
count = 0
for input in inputs:
grad_conv = np.zeros(weight.shape[0],)
for i in range(weight.shape[0]):
a = 0
for j in range(fmap_width):
a += input[j+i]
grad_conv[i] = a
out = grad_conv[np.newaxis, :]
if count == 0:
outs = out.copy()
else:
outs = np.concatenate((outs, out))
count += 1
return outs
def loss_gradient(inputs, targets):
_, pred, fc, conv = forward(inputs, targets) # _, (1, batch), (1, batch), (7, batch)
Y = np.transpose(targets, (1, 0)) # (batch, 1) -> (1, batch)
dL_dsig = -1*( (Y / pred) - ( (1-Y) / (1-pred) ) ) # (1, batch)
#print(dL_dsig)
dsig_dfc = ( 1/(1+np.exp(-fc)) ) * ( 1 - 1/(1+np.exp(-fc)) ) # (1, batch)
#print(dsig_dfc)
dfc_dWl = np.transpose(conv, (1, 0)) # (batch, 7)
#print(dfc_dWl)
# dfc_dBl = np.ones_like(fc) (1, batch) 어차피 1인 요소인 항등원이므로 없어도 무방합니다.
# Wl, Bl 을 구해봅시다.
dL_dfc = dL_dsig * dsig_dfc # (1, batch)
# print(dL_dfc)
dL_dWl = np.dot(dL_dfc, dfc_dWl) # (1, 7)
#print(dL_dWl)
dL_dBl = np.sum(dL_dfc, keepdims=True) # (1, 1)
#print(dL_dBl)
dfc_dconv = np.transpose(Wl, (1, 0)) # (7, 1)
#print(dfc_dconv)
dconv_dWc = gradient_conv(inputs, Wc) # (batch, 3)
#print(dconv_dWc)
# dconv_dWc = np.ones_like(np.transpose(conv, (1, 0))) # conv의 원래 형태인 (batch, 7)에서 1인 요소인 항등원이므로 없어도 무방
# Wc, Bc 를 구해봅시다.
dL_dconv = np.dot(dfc_dconv, dL_dfc) # (7, batch)
#print(dL_dconv)
dL_dWc = np.sum(np.dot(dL_dconv,dconv_dWc), axis=0) # (3, )
#print(dL_dWc)
dL_dBc = np.sum(dL_dconv)
#print(dL_dBc)
return dL_dWl, dL_dBl, dL_dWc, dL_dBc
learning_rate = 0.05
epochs = 600
for epoch in range(epochs+1):
dL_dWl, dL_dBl, dL_dWc, dL_dBc = loss_gradient(X, Y)
Wl = Wl + -1*learning_rate*dL_dWl
Bl = Bl + -1*learning_rate*dL_dBl
Wc = Wc + -1*learning_rate*dL_dWc
Bc = Bc + -1*learning_rate*dL_dBc
if epoch % 60 == 0:
loss, pred, _, _ = forward(X, Y)
print('epoch :', epoch, '\n', 'pred :' , pred, '\n', 'loss :', loss)'파이썬 프로그래밍 > Numpy 딥러닝' 카테고리의 다른 글
| 31. [CNN기초] 2차원 배열 합성곱 - image to column-2 (0) | 2023.01.11 |
|---|---|
| 30. [CNN기초] 2차원 배열 합성곱 - image to column 구현 (0) | 2023.01.06 |
| 28. [CNN기초] 1차원 배열 CNN 훈련하기-2(배치구현) (0) | 2023.01.04 |
| 27. [CNN기초] 1차원 배열 CNN 훈련하기-1 (0) | 2023.01.03 |
| 26. [CNN기초] CNN 개요 (0) | 2023.01.01 |



